Формула как найти объем бруска – Вычислите объем деревянного бруска, имеющего форму прямоугольного ,параллелепипеда если его измерения равны 2,5 см; 4

Брус и брусок — расчёт м3 и шт, таблица, калькулятор

Что является бруском, а что брусом?

Исходя из уменьшительного названия — брусок, можно сделать вывод что это нечто меньшее чем брус. Где именно проходит граница? Брус это пиломатериал с толщиной больше 100 мм. Брусок — пиломатериал с толщиной менее 100 мм, но при том ширина не должна превосходить толщину в 2 раза. Иначе это уже будет доска.
Брусок зачастую изготавливается с размером стороны от 20 мм. Если порода дерева мягкая, то как правило не превышает длины 2 метра. Для остальных брусков предельная длина 6,5 метров.

Таблица объёма бруса и брусков и количества штук в кубическом метре

Кубатурник брусков и бруса.
Обратите внимание!
1. Все расчёты приведены для 1 метра. Это сделано для простоты перевода во все прочие длины и снижения размера таблицы.
2. Можно настроить количество строк на странице, нажав на стрелку вниз «Показать 10 записей».
3. Воспользоваться поиском, введя значение справа.
4. Ниже таблицы расположен калькулятор

Брус размеры, мм	Кубов в 1 шт	Штук в кубе	Брусок размеры, мм	Кубов в 1 шт	Штук в кубе
100х100х1000	0,01	100	20х30х1000	0,0006	1666,7
100х120х1000	0,012	83,3	25х25х1000	0,000625	1600
100х140х1000	0,014	71,4	25х30х1000	0,00075	1333,3
100х150х1000	0,015	66,7	25х35х1000	0,000875	1142,9
100х160х1000	0,016	62,5	25х40х1000	0,001	1000
100х175х1000	0,0175	57,1	25х45х1000	0,001125	888,9
100х180х1000	0,018	55,6	30х30х1000	0,0009	1111,1
100х200х1000	0,02	50	30х40х1000	0,0012	833,3
100х220х1000	0,022	45,5	30х45х1000	0,00135	740,7
100х240х1000	0,024	41,7	30х50х1000	0,0015	666,7
100х250х1000	0,025	40	35х35х1000	0,001225	816,3
100х300х1000	0,03	33,3	35х40х1000	0,0014	714,3
100х300х1000	0,03	33,3	35х50х1000	0,00175	571,4
100х400х1000	0,04	25	35х60х1000	0,0021	476,2
115х115х1000	0,013225	75,6	40х40х1000	0,0016	625
120х120х1000	0,0144	69,4	40х45х1000	0,0018	555,6
120х150х1000	0,018	55,6	40х50х1000	0,002	500
120х180х1000	0,0216	46,3	40х60х1000	0,0024	416,7
120х200х1000	0,024	41,7	40х70х1000	0,0028	357,1
125х125х1000	0,015625	64	45х45х1000	0,002025	493,8
125х200х1000	0,025	40	45х50х1000	0,00225	444,4
130х130х1000	0,0169	59,2	45х60х1000	0,0027	370,4
135х135х1000	0,018225	54,9	45х70х1000	0,00315	317,5
140х140х1000	0,0196	51	50х50х1000	0,0025	400
140х160х1000	0,0224	44,6	50х55х1000	0,00275	363,6
140х190х1000	0,0266	37,6	50х60х1000	0,003	333,3
145х145х1000	0,021025	47,6	50х70х1000	0,0035	285,7
145х195х1000	0,028275	35,4	50х75х1000	0,00375	266,7
150х150х1000	0,0225	44,4	50х80х1000	0,004	250
150х200х1000	0,03	33,3	50х90х1000	0,0045	222,2
150х200х1000	0,03	33,3	50х100х1000	0,005	200
150х250х1000	0,0375	26,7	55х55х1000	0,003025	330,6
150х250х1000	0,0375	26,7	60х60х1000	0,0036	277,8
150х300х1000	0,045	22,2	60х70х1000	0,0042	238,1
160х160х1000	0,0256	39,1	60х80х1000	0,0048	208,3
160х200х1000	0,032	31,3	60х90х1000	0,0054	185,2
170х170х1000	0,0289	34,6	60х100х1000	0,006	166,7
170х200х1000	0,034	29,4	60х110х1000	0,0066	151,5
175х175х1000	0,030625	32,7	65х65х1000	0,004225	236,7
175х250х1000	0,04375	22,9	70х70х1000	0,0049	204,1
180х180х1000	0,0324	30,9	70х80х1000	0,0056	178,6
180х200х1000	0,036	27,8	70х100х1000	0,007	142,9
180х220х1000	0,0396	25,3	70х120х1000	0,0084	119
180х240х1000	0,0432	23,1	75х75х1000	0,005625	177,8
185х200х1000	0,037	27	75х100х1000	0,0075	133,3
190х190х1000	0,0361	27,7	75х125х1000	0,009375	106,7
195х145х1000	0,028275	35,4	80х100х1000	0,008	125
195х195х1000	0,038025	26,3	80х120х1000	0,0096	104,2
200х200х1000	0,04	25	80х140х1000	0,0112	89,3
200х240х1000	0,048	20,8	80х150х1000	0,012	83,3
200х250х1000	0,05	20	80х160х1000	0,0128	78,1
200х300х1000	0,06	16,7	90х100х1000	0,009	111,1
200х400х1000	0,08	12,5	95х145х1000	0,013775	72,6
220х220х1000	0,0484	20,7
225х225х1000	0,050625	19,8
230х230х1000	0,0529	18,9
240х240х1000	0,0576	17,4
250х300х1000	0,075	13,3
260х260х1000	0,0676	14,8
280х280х1000	0,0784	12,8
300х300х1000	0,09	11,1
300х500х1000	0,15	6,7
400х400х1000	0,16	6,3
450х450х1000	0,2025	4,9
500х500х1000	0,25	4

Можно рассчитать объём любого предмета, который является брусом или же доской. В геометрии такой объект является прямоугольным параллелепипедом.

Как посчитать самому объём бруса?

• Формула следующая: высота * ширина * длина
  • Для примера возьмём брус с такими значениями:
    • 200 мм ширина
    • 200 мм высота
    • 6000 мм длина
  • Обязательно перевести все значения метры, ведь мы хотим узнать метры кубические, а исходные данные в миллиметрах.
  • Значит 200 мм умножаем на 0,001 — тем самым сокращаем значение в 1000 раз, поскольку метр больше миллиметра в 1000 раз. В одном метре 0,001 мм, иными словами.
  • Получим: 0,2 * 0,2 * 6 = 0,24 кубических метра занимает один брус.
  • Ну и в завершении можно умножить на количество имеющегося для расчёта бруса и получить объём всей партии, главное чтоб длина каждого бруса была одинаковой. Иначе получится ошибка. А что если длина всех брусов разная?
• Следующий вариант для такого случая
  • Например:
    • 15 брусов длиной 4 метра
    • 5 брусов длиной 6 метров
    • 10 брусов длиной 3 метра
  • Сначала получим общую длину: (15 * 4) + (5 * 6) + (10 * 3) = 120 метров совокупная длина.
  • Вот вместо длины одного бруска подставим это значение длины и получим общую кубатуру разных по длине
• брусков. Главное, чтобы ширина и высота оставались при этом у всех одни и те же.

Непонятно, сложно? Не проблема! Добавьте в закладки эту страницу, чтобы всегда можно было рассчитывать на быстрый и точный расчёт.

Как перевести из куба в штуки?

1. Вычисляем объём 1 единицы пиломатериала
2. Делим 1 на получившееся значение, тем самым узнаём количество штук бруса или бруска в 1м3

• Например:
  • Брус 120х120 мм и длиной 3 метра, занимает объём 0,0432 кубометра
  • 1 делим на 0,0432 и получаем 23,14 — такое количество бруса поместится в 1 кубический метр

Какая цена бруса?

• Зависит от породы дерева и региона. Но во всех случаях цена выше если:
  • Дерево прошло сушку +20% к цене
  • Брус клееный, стыкованный +80+100% к цене
  • Доставка — зависит от индивидуального случая
  • Струганный может быть дороже на 20 или 30%
  • Сортность древесины может увеличить цену кратно
  • Прочая любая механическая или химическая обработка от 20%
• Цены 1м3 простого бруса естественной влажности из разных пород дерева и в зависимости от продавца, например:
  • Сосна и ель — 9 тыс руб +-15%
  • Лиственница и дуб на — 12-16 тыс руб за м3 +-10%
  • Липа на 70-80% дороже — 17-18 тыс руб за м3 +-10%

Онлайн калькулятор: Объем геометрических фигур

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

Формула:

Объем куба

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

save Сохранить share

Поделиться extension Виджет

Объем прямоугольной призмы

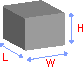Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

save Сохранить share Поделиться extension Виджет

Объем пирамиды

Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания

Точность вычисления

Знаков после запятой: 5

save Сохранить share Поделиться extension Виджет

Объем усеченной пирамиды

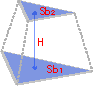Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Точность вычисления

Знаков после запятой: 5

ФИЗИКА: Задачи на плотность, массу и объем

Задачи на плотность, массу и объем с решением

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины	Обозначение	Единицы измерения	Формула
Масса	m	кг	m = p * V
Объем	V	м3	V = m / p
Плотность	p	кг/м3	p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

---

 

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.  Найдите плотность молока, если 206 г молока занимают объем 200 см³?

---

Задача № 2.  Определите объем кирпича, если его масса 5 кг?

---

Задача № 3.  Определите массу стальной детали объёмом 120 см³

---

Задача № 4.  Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м³) меньше плотности стали (ρ₁ = 7800 кг/м³). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

---

Задача № 5.  Определите плотность мела, если масса его куска объемом 20 см³ равна 48 г. Выразите эту плотность в кг/м³ и в г/см³.

Ответ: Плотность мела 2,4 г/см³, или 2400 кг/м³.

---

Задача № 6.  Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м³ • 0,04 м² • 5 м = 160 кг.

---

Задача № 7.  Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

---

Задача № 8 (повышенной сложности).  Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а³ = 216 см³. Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р:   V_С = m_К / р = 91 см³. Следовательно, объем полости V_П = V_K — V_C = 125 см³. Поскольку 125 см³ = (5 см)³, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

---

Задача № 9 (олимпиадный уровень).  Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м³

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

 

---

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

 

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

1. Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
2. Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
3. Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
4. Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
5. Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
6. Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
7. Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

 

---

Конспект урока «Задачи на плотность, массу и объем с решением».

Следующая тема: «Задачи на силу тяжести и вес тела».

 

Масса сплошной детали | Математика для ювелиров

9.05.2013 // Владимир Трунов   

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

---

1. Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:

---

2. Масса цилиндра

Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:

---

3. Масса шара

Объем шара: , где — диаметр шара.
Тогда масса:

---

4. Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:

---

5. Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:

---

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

---

7. Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:

---

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

---

Как рассчитать объём пиломатериала. Общие инструкции: как рассчитать кубатуру доски.

Будь вы столяр или просто закупаете необходимый объем кубатуры пиломатериалы исходя из расчетов, умение правильно рассчитать объем пиломатериала поможет в правильном составлении сметы и убережет от дополнительных финансовых расходов.

Дополнительная необходимость в том, чтобы научиться считать объем пиломатериала также исходит из того, что это практически единственный вид строительного материала, который продается не поштучно или на развес, а в кубометрах.

На качество, вес и стоимость пиломатериала влияет множество факторов, поверхность древесины (наличие скол, шлифовальные работы, обжиг, трещины и т.д), влажность и способ распила, который может быть тангенциальным и радиальным.

Виды пиломатериала

На сегодняшнем рынке представлено множество видов пиломатериалов, которые различаются способом изготовления и эксплуатационными характеристиками:

• Брус. Пиломатериал с чаще всего квадратным сечением, толщина и ширина которого больше или меньше 100 мм. Применяется повсеместно для строительства жилья и сооружений, а также в качестве несущих конструкций
• Горбыль. Боковой фрагмент бревна, одна сторона которого обработана, а другая не пропилена или обработана лишь частично. Используется для сооружения заборов, опалубки, для настила на пол, а также в декоративных целях



• Обапол. В нем обработана лишь внутренняя часть, обычно это начальный или последний срез бревна. Его можно использовать для настила на пол и кровли крыш, а также для отделки фасада и интерьера помещений
• Доска. Это пиломатериал прямоугольной формы. Может использоваться для опалубки, стропила для крыши, для строительства стен и пола и во многих других сферах строительства. Доска может быть обрезной и необрезной

Общие инструкции: как рассчитать кубатуру доски

Конечно проще, когда пиломатериал расфасован по упаковкам с точными указаниями цены и объема, но подобное встречается довольно редко и занимаются этим компании выпускающие большие партии продукции по высоким ценам. Ценник за доску у частников обычно ниже, но и доски поставляются обычно скопом без четкой расфасовки. Важно всегда покупать партию немного большей кубатуры, чем необходимо, так как в процессе строительных работ, скорее всего, обнаружится, что пиломатериала не хватает, а часть продукции в партии бракованная.

Расчеты по одному кубу доски будут различаться в зависимости породы дерева, а также уровне обработки пиломатериала. Необрезная и обрезная доска рассчитываются по разным формулам. Что касается породы, то проще всего посчитать один куб древесины из хвойных пород: замеряются и перемножаются ширина, длина и толщина одной доски, а затем получившиеся показатели умножаются на количество идентичного пиломатериала.

Как рассчитать объем пиломатериала: необрезной доски

Необрезная доска получается путем продольного распила бревен без дополнительной обработки досок по бокам. Такой пиломатериал дешевле, чем обрезные доски, но их недостаток кроется в сложном произведении расчетов куба продукции. В отличие от обрезных досок, не получится рассчитать общий объем пиломатериала исходя от габаритов одной доски, так как в зависимости от доски различается ее ширина, идентичной остается только длина и ширина. Различия в ширине происходят из-за того что необрезные доски выпиливаются из разных участков бревна.

Куб необрезной доски можно рассчитать двумя способами:

1 способ

В необрезных досках часто встречается непропорциональность между толщиной и шириной доски на ее разных концах, поэтому для правильных расчетов необходимо определить минимальные и максимальные значения ширины и толщины доски. Получившиеся результаты делим на 2. Сама формула будет выглядеть подобным образом: (a1+a2)/2*(b1+b2)/2*c. При необходимости в правильных расчетах может пригодиться калькулятор. К единственному недостатку подобного способа можно отнести высокие затраты времени, т.к. из-за того, что доски меду собой отличаются, придется производить замеры каждой единицы пиломатериала отдельно.

2 способ

Гораздо проще произвести расчеты, когда необходимо доской обшить какую-то часть здания, будь то пол или стена. Для этого берем площадь, которую необходимо отделать доской, и умножаем ее на толщину обшивочного материала – полученное число и будет требуемым объемом пиломатериала. Для большего понимания приведем пример: для облицовки стены здания параметрами 8*4 с высотой 4 метра используем доску толщиной 20 мм.

Вычисляем площадь стены, а именно: (8+8+4+4)*4=96 кв.м. Далее получивший результат перемножаем с толщиной необрезной доски и у нас получается: 95*0,020=1,9 кб.м. Ширина доски не имеет никакого значения, на расчеты это не оказывает никакого влияния. Но при этом для произведения строительных работ не будет лишним узнать средние значения доски в зависимости от ее длины. Усредненные данные вы можете увидеть на таблице ниже.

Как посчитать объем пиломатериала: обрезная доска

Обрезная доска – это наиболее ходовой вид пиломатериала, который немного дороже обрезной доски, т.к. древесина обрабатывается со всех сторон. Для ее получения бревно продольно распиливают на доски, а потом уже обрабатывают боковые грани, получившийся материал имеет прямоугольную форму. К преимуществам данного лесопильного материала относят большую долговечность, так как вместе с корой удаляют вредные микроорганизмы, а также улучшение стыковки с другими лесопильными материалами за счет очищенных сторон.

Обрезные доски проходят дополнительную сушку и множество операций по обработке, за счет которых повышается не только их эксплуатационные характеристики, но и цена. На цену также влияет порода древесины и сорт пиломатериала.

Так как обрезные доски идентичны между собой по размерам, то расчет кубатуры будет производиться по простой формуле: V=l*h*a, где l,h,a -это длина, высота и ширина соответственно, а V- объем.

Как рассчитать объем бруса

В строительстве чаще всего используют брус с квадратным сечением, то есть с соотношением сторон 100*100 мм. Чтобы вычислить кубатуру одного бруса необходимо произведение его ширины и высоты умножить на длину бруса. Для примера рассмотрим случай, когда необходимо приобрести 30 единиц бруса с сечением 100*100 мм и длиной 9 метров. Для этого перемножаем ширину на высоту, а получившееся значение умножаем на длину одного бруса. В целом расчеты будут выглядеть подобным образом: 0,10*0,10*9=0,09 м3 – такова будет кубатура одного бруса. Теперь умножаем это значение на количество необходимо бруса, получается: 0,09*30=2,7 м3 .

Если в брусе имеются пазы, то это зачастую никоим образом не влияет на кубатуру, так как продукция в партии пиломатериала плотно соединена между собой.

Общие выводы

Вычислить необходимое количество кубометров пиломатериала вовсе несложно, если известны формулы для расчетов. Уже после измерений вам станет намного легче вычислить необходимое количество кубометров и быстро узнать его стоимость.

Вам понравится

по какой формуле высчитать объём бревна? всё перерыл, нигде не нашел!

Объем бревна (без коры) V вычисляют по формуле: <img src=»//otvet.imgsmail.ru/download/bb233527e6dcc1422b335c53e01c123f_i-792.gif» > где: V- объем бревна, м3, L- длина бревна, дм, D- нижний диаметр, см, d- верхний диаметр, см Для коэффициента а формулы применяют следующие значения: Верхний диаметр, см до 14 вкл. 0,485 0,485 0,485 от 15 до 24 0,465 0,460 0,455 25 и более 0,440 0,430 0,420 в зависимости от Длины бревна, дм до 34,9 вкл. от 35,0 до 44,9 45,0 и более на практике гораздо проще пользоваться таблицами <a rel=»nofollow» href=»http://les4you.ru/kubatura-brevna.html» target=»_blank»>http://les4you.ru/kubatura-brevna.html</a>

А чё, объём цилиндра не устраиваит?

По формуле объема цилиндра.

Площадь круга (пи*R квадрат) умножить на высоту (длину бревна) . P.S.: R — радиус (диаметр пополам)

<a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Цилиндр» target=»_blank»>http://ru.wikipedia.org/wiki/Цилиндр</a>

Пи * R в квадрате * h Пи= 3,141 примерно R — радиус h- длина бревна

Вывести среднее арифметическое диаметров конца бревна и его начала. И далее считать, как объем цилиндра.

По формуле усеченного конуса. Нижнее основание -комель, верхнее -отрубь. Радиусы комеля, отруби и длину знаете, считайте. <img src=»//otvet.imgsmail.ru/download/8c907696f5a7c8874b98540ef99ac532_i-245.jpg» > R — радиус комеля; r — радиус отруби; h — длина бревна п = 3,14

бревно, это не цилиндр, а усеченный конус. Объем бревна определяется, на практике, по таблицам (кубатурник)