F-профиль| L-профиль | стартовый профиль для откосов
Наша компания, предлагает Вам высококачественные комплектующие к панелям ПВХ. Предлагаемые комплектующие способны придать любому помещению, в котором проводились те или иные отделочные работы, — законченный вид, скрыть многие недостатки, возникающие при монтаже, к примеру, подоконник и оконный проем.
Мы предлагаем Вам на выбор большой перечень комплектующих, способных существенно облегчить работу с панелями ПВХ широкий F-образный профиль (F-профиль), молдинги ПВХ, внутренний и наружный угол, соединительный профиль (Н-профиль), L-профиль, плинтус карниз(J-профилем и фаска).
F-профиль
F-профиль предназначен для обрамления торцевых углов поверхностей сэндвич или пластиковых панелей, к примеру при отделке оконных и дверных проемов.
На фото представлен один из цветовых вариантов изготавливаемого нами F-профиля.
Наружный угол
Наружный угол соединяет пластиковые панели на внешних углах и скрывает стеновой угол.
Внутренний угол
Внутренний угол соединяет панели ПВХ по внутренним углам и отделывает фронтальные стороны углов примыкания двух поверхностей. Скрывает угол от соединения двух стен и стеновых панелей, расположенных на них.
L-профиль — стартовый профиль для откосов
L-профиль имеет Г-образную форму, применяется для мест примыкания панелей ПВХк дверным и оконным проемам и торцевых граней пластиковых панелей.
Установка пластиковых панелей ПВХ начинается именно с данного профиля — панель вставляется в паз.
У нас, L-профиль изготавливается на импортном оборудовании из высококачественных материалов. Мы изготавливаем профиль шириной 5 и 10 мм.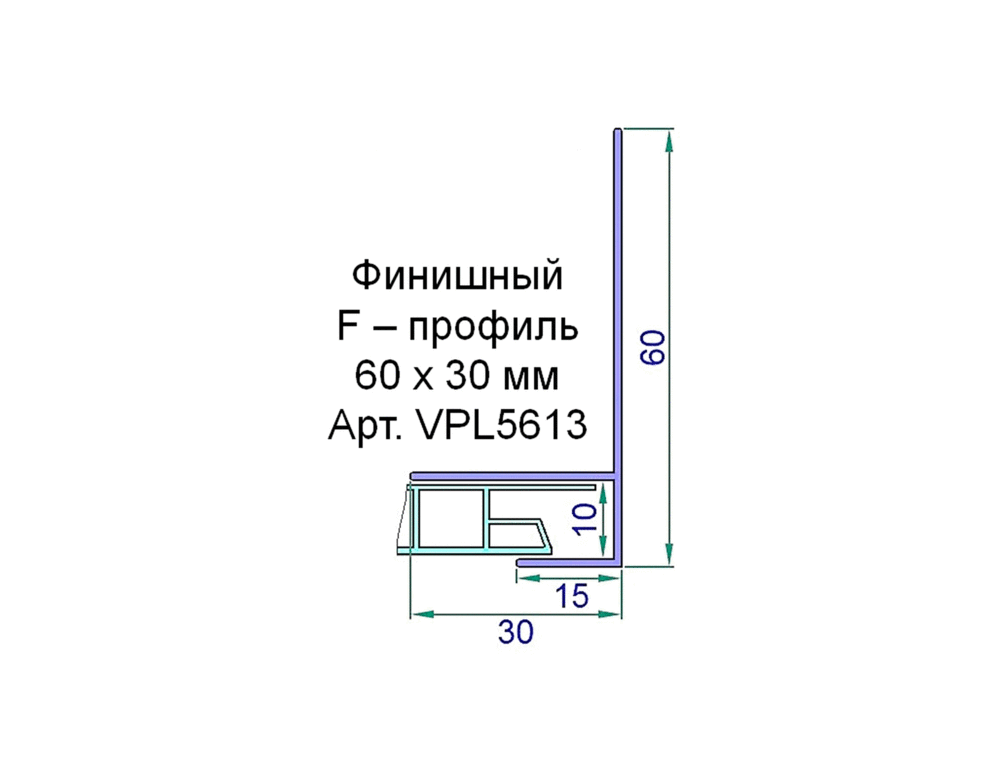
Стартовый профиль для откосов от МСК ПЛАСТИК, это всегда высокое качество по разумным ценам. Данный вид продукции, как впрочем и всё остальное, постоянно имеется в наличии на наших складах. Стоимость профиля можно уточнить по телефону в разделе контакты.
Соединительный профиль
Соединительный профиль имеет форму балки. Стыкует пластиковые панели по вертикали или горизонтали между собой.
Плинтус потолочный
Плинтус потолочный надежно крепит панель по горизонтали на стену, благодаря П-образной направляющей и идеально скрывает стык между стеной и потолком в виде декоративной планки, в виде обычного плинтуса.
РАЗМЕРЫ:
5 мм и 10 мм
Виды стартовых профилей для откосов: I-профиль, F-профиль, L-профиль.
 I-профиль для откосов
I-профиль для откосов Крепление I-профиля производится на стену, к которой планируется прикреплять откосы. Для этого используются обычные саморезы. Выполнен данный профиль в форме буквы «I», что предоставляет массу удобств во время его монтирования.
I-профиль широко используется для откосов из гипсокартона или различных декоративных материалов. Благодаря универсальной конструкции этого профиля его монтаж произвести достаточно легко.
Форма профиля позволяет крепить его к оконному проему в любом положении. Главное, чтобы он располагался перпендикулярно к оконной раме. На стыках профиля его необходимо обрезать под соответствующим углом.
Стыки заделываются специальной строительной шпатлевкой, что предотвратит возможность проникновения в помещения влаги и холода.
При монтировании данного профиля необходимо изначально произвести замер оконного проема. Для этого можно использовать строительную рулетку. Данное действие поможет максимально точно вырезать необходимый профиль.
Данное действие поможет максимально точно вырезать необходимый профиль.
Крепеж необходимо производить по самому краю оконного профиля. Таким образом, закрепление профиля производится на окне. Закрепление профиля производится исключительно в местах будущих откосов.
F-профиль для откосовДанный профиль выполнен в форме буквы «F», что предоставляет массу удобств во время его монтирования. С его помощью можно производить монтаж:
- Пластиковых откосов;
- Откосов из сэндвич-панелей;
- Откосов из декоративных материалов;
- Откосов из гипсокартона.
Установка профиля производится по всему периметру окна. На стыках профиль необходимо обрезать под углом в 45 градусов, что обеспечит идеально ровные стыки и позволит максимально точно произвести установку откосов.
Монтаж F-профиля производится только после полной очистки поверхности. Далее производится запенивание зазоров и срезание лишней пены.
С этой целью можно использовать специальный строительный нож.
Очень часто F-профиль сажают на специальную клеевую основу. Но такой монтаж профиля является ошибкой, так как со временем в местах соединения могут возникнуть щели, через которые в помещение будет проникать холод.
L-профиль для откосовL-профиль применяют для монтирования пластиковых откосов. С помощью этого профиля можно монтировать панели из гипсокартона, толщина которого составляет 10 миллиметров. Также этот профиль используется для монтажа пластиковых откосов.
Установка этого профиля перпендикулярно к окну и имеет минимальный разворот. L-профиль необходимо прикреплять перпендикулярно вдоль края. При этом расстояние между саморезами должно составлять около 15 сантиметров.
При установке откосов необходимо изначально прикрутить верхний профиль по всей ширине рамы окна. Далее производится монтаж боковых профилей, а после этого нижний профиль.
При установке этого профиля необходимо помнить, что узкую полочку профиля необходимо обращать внутрь окна, а широкую к стенкам проема. Это обеспечит надежное крепление откосов в дальнейшем.
Это обеспечит надежное крепление откосов в дальнейшем.
При установки этого профиля необходимо использовать строительный уровень. Это позволит соорудить откосы максимально ровно. Откосы вставляются в специальные пазы профиля, что значительно упрощает процесс монтажа.
Также вам будет интресно:
Профиля являются неотъемлемым атрибутом при установке откосов. С их помощью можно произвести максимально ровную установку, что придаст окну правильную форму.
Также посмотрите полезное видео о монтаже оконного профиля
Твитнутьописание ПВХ-профиля для панелей, размеры и цвета. Для чего нужен?
Среди многих вариантов оформительских изделий важную роль играет пластиковый F-образный профиль. Разобраться с особенностями этого ПВХ-профиля для панелей необходимо, конечно, ещё до заказа или покупки. Существуют различные размеры и цвета таких изделий, однако следует четко представлять, для чего же нужен сам профиль.
Разобраться с особенностями этого ПВХ-профиля для панелей необходимо, конечно, ещё до заказа или покупки. Существуют различные размеры и цвета таких изделий, однако следует четко представлять, для чего же нужен сам профиль.
Что это такое?
Необходимо отметить, что пластиковый F-образный профиль изготавливают не из неких абстрактных пластиков, а из строго конкретного ПВХ. В основном его используют для монтажа пластиковых окон. Идентичность теплового расширения оказывается очень серьезным преимуществом, поскольку конструкции не будут деформироваться. В пользу подобных изделий свидетельствует и легкость установки, если сравнивать с альтернативными техническими решениями. Более подробную информацию можно получить только применительно к конкретной модели. Главное заключается в том, что все они рассчитаны на многоразовое использование.Размеры и цвета
В подавляющем большинстве случаев такие изделия окрашивают в белый цвет.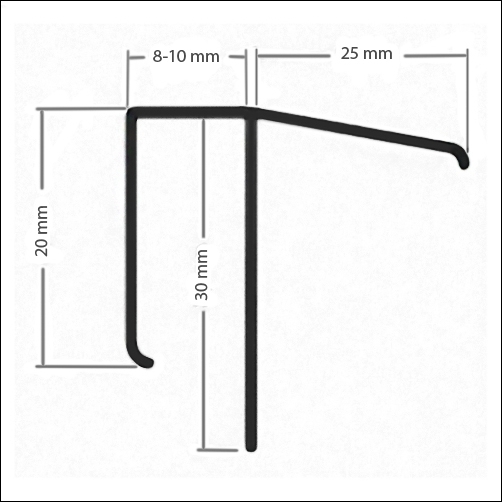
Кроме того, даже при использовании окон другой окраски белый тон отлично впишется в обстановку благодаря своей универсальности. Но если использовать ламинированные покрытия, то никаких проблем с приданием другой расцветки не возникнет.
Ее можно даже изменять в процессе эксплуатации, например, используя следующие цвета:
-
темно-серый;
-
ярко-желтый;
-
светло-зеленый;
-
светло-коричневый;
-
орех;
-
лимонный;
-
красное дерево;
-
морская волна.
Однако окрас профиля должен соответствовать фасаду дома. Если жилище оформляется в классическом стиле, то бессмысленно (и даже вредно) употреблять кричащие цвета. Более приемлемы древесные оттенки. Если они не нравятся, можно рассмотреть вариант с неяркими, приглушенными красками. Обязательно нужно следить за сочетаемостью выбранной расцветки с тоном дверей и кровли.
Если жилище оформляется в классическом стиле, то бессмысленно (и даже вредно) употреблять кричащие цвета. Более приемлемы древесные оттенки. Если они не нравятся, можно рассмотреть вариант с неяркими, приглушенными красками. Обязательно нужно следить за сочетаемостью выбранной расцветки с тоном дверей и кровли.
Что касается габаритов, то тут многое зависит от производителя. Например, один из малых вариантов молдинга имеет полку величиной 10 мм. В этом случае его общие размеры могут составлять 3000х10х60 мм. А также в продаже встречаются варианты (в мм):
-
18х40х25;
-
20х60х22;
-
25х60х3000;
-
35х35х3000.
Именно поэтому при выборе стоит уточнять, что значит то или иное число в маркировке изделия.
Для чего он нужен?
Угловой профиль в виде буквы «F» используют для панелей, монтируемых на стены. Его основное назначение в этом случае — декорирование внутренних и внешних углов. Конструкция перекроет щели и зазоры между плитами, пропускающие влагу или нарушающие внешний вид постройки. Панели будут отлично соединены по всей длине. Некоторые модели предназначаются под монтаж пластикового откоса из сэндвич-панелей.
Такие изделия обеспечивают идеальное примыкание к поверхности.
Что немаловажно, вместе с этим профиль оказывается еще и финишной частью отделки. Он визуально завершает композицию, придает требуемую эстетичность. Подобные изделия нужны, чтобы обустраивать углы свыше 90 градусов. Обычно такие конструкции делаются из материалов, стойких к воздействию солнечного света и отличающихся большой эластичностью.
Он визуально завершает композицию, придает требуемую эстетичность. Подобные изделия нужны, чтобы обустраивать углы свыше 90 градусов. Обычно такие конструкции делаются из материалов, стойких к воздействию солнечного света и отличающихся большой эластичностью.
Полностью облицевать поверхность панелями из ПВХ можно с использованием различных доборных элементов. Они обеспечивают качественный и надежный монтаж. Следует понимать, что профиль в виде буквы «F» является лишь одним из таких элементов, поэтому должен применяться в связке с другими деталями. Планки такого рода монтируются без использования клея. Если потребуется, например, наклеить обои, достаточно будет просто демонтировать на время работ планку, а затем вернуть ее на прежнюю позицию.
Как крепить?
Эта работа не вызывает каких-либо сложностей. Профильные полосы просто подрезают на нужную длину. Затем их фиксируют на пазы. Часть людей пользуется жидким клеем, но так действовать стоит только в одном случае — когда понятно, что больше не придется снимать конструкцию. Во всех других ситуациях такой шаг лишь усложнит процесс и создаст потом дополнительные трудности.
Профильные полосы просто подрезают на нужную длину. Затем их фиксируют на пазы. Часть людей пользуется жидким клеем, но так действовать стоит только в одном случае — когда понятно, что больше не придется снимать конструкцию. Во всех других ситуациях такой шаг лишь усложнит процесс и создаст потом дополнительные трудности.
Иногда в процессе установки профиля появляются незначительные щели. Устранить их помогает покрытие белым силиконом. Профиль начинают устанавливать с верхней части откоса, постепенно идя вниз. По краям профиля после отпила на нужную величину отмечают карандашом отступы по 50 мм. Эти участки надо будет раскроить под углом 45 градусов. Никаких проблем даже для неопытных людей возникать с монтажными работами по установке профиля не должно.
Профили для откосов F и П
Наши профиля помогут сделать монтаж откосов окна качественно и красиво.
Тщательно подобранные компоненты исходного сырья гарантируют стабильный цвет изделий, удобство в работе и долговечность.
Профиля имеют кремовый оттенок, который специально подбирался для соответствия большинству профилей и откосных сэндвич панелей.
С радостью передадим вам образцы и сделаем ценовое предложение.
При отделке помещений пластиковыми панелями, откосами, подоконниками необходимы специальные аксессуары, помогающие при монтаже и для декоративных целей.
Ассортимент профилей ПВХ:
Код | Профиль | Наименование | Длина | Цвет |
1001 |
| Соединительный профиль | 3м | Белый |
901 | Стартовый профиль 20 мм. | 3м | Белый | |
923 | 3м | Золотой дуб | ||
924 | 3м | Махагон | ||
2701 |
| Закрывающий профиль внешний 10×60 | 3м, 6м | Белый |
2901 |
| Закрывающий профиль 25×45 | 3м, 6м | Белый |
2601 |
| Закрывающий профиль 10×45 | 6м | Белый |
2623 | 3м | Золотой дуб | ||
2624 | 3м | Махагон |
Универсальный угол ПВХ в защитной пленке
Для изготовления универсальных уголков используются листы жесткого пластика ПВХ.
Размеры (мм): 10 х 20; 20 х 20; 20 х 40; 25 х 25; 30 х 30; 35 х 35; 40 х 40; 50 х 50; 60 х 60.
Длина: 3м
Цвет: белый
Упаковка: 50шт
Цветные откосы Crystallit
Цветные откосы для окон Crystallit — это уникальные изделия, выполненные из высококачественных и утепленных сэндвич-панелей с акриловым покрытием. Покрытие выполнено из плёнки Elesgo, абсолютно того же материала, что используется при производстве подоконников Crystallit. Таким образом, все характеристики УФ-стойкости, прочности, долговечности распространяются и на откосные системы Crystallit. Использование одного и того же покрытия даёт ещё одно неоспоримое преимущество: цвет откосов в точности совпадает с цветом подоконника. Купить откосы Кристаллит можно как с подоконниками, так и отдельно. Откосная система состоит из всех необходимых комплектующих – стартовый П и финишный F профили, повторяющими декор. F-профиль выполнен в двух ширинах. Все решения вкупе облегчают монтаж и позволяют придать окну с откосами законченный, гармоничный вид и позволяет сделать оконный проём монолитной конструкцией.
F-профиль выполнен в двух ширинах. Все решения вкупе облегчают монтаж и позволяют придать окну с откосами законченный, гармоничный вид и позволяет сделать оконный проём монолитной конструкцией.
Белый глянец | Кремовый глянец | Дуб белый матовый |
Дуб белый глянец | Мрамор матовый | Мрамор глянец |
Дуб натуральный матовый | Дуб натуральный глянец | Дуб золотой матовый |
Дуб золотой глянец | Орех матовый | Орех глянец |
Махагон матовый | Махагон глянец | Венге матовый |
Венге глянец | Антрацит матовый | Белый матовый |
Сэндвич-панели и профили изготавливаются строго по размерам:
ширина от 150 мм до 700 мм
длина фиксированная — 1000, 1500, 1700, 2000, 2200, 2400, 2600, 3000 мм
Цены на откосы указаны в рублях за 1 шт. :
:
Белый матовый, мрамор матовый, белый дуб матовый, натуральный дуб матовый, золотой дуб матовый, орех матовый, венге матовый, махагон матовый.
| ширина / длина мм | 1000 | 1500 | 1700 | 2000 | 2200 | 2400 | 2600 | 3000 |
| ширина 150 мм | 600 | 900 | 1020 | 1200 | 1320 | 1440 | 1560 | 1800 |
| ширина 200 мм | 800 | 1200 | 1360 | 1600 | 1760 | 1920 | 2080 | 2400 |
| ширина 250 мм | 1000 | 1500 | 1700 | 2000 | 2200 | 2400 | 2600 | 3000 |
| ширина 300 мм | 1200 | 1800 | 2040 | 2400 | 2640 | 2880 | 3120 | 3600 |
| ширина 350 мм | 1400 | 2100 | 2380 | 2800 | 3080 | 3360 | 3640 | 4200 |
| ширина 400 мм | 1600 | 2400 | 2720 | 3200 | 3520 | 3840 | 4160 | 4800 |
| ширина 450 мм | 1800 | 2700 | 3060 | 3600 | 3960 | 4320 | 4680 | 5400 |
| ширина 500 мм | 2000 | 3000 | 3400 | 4000 | 4400 | 4800 | 5200 | 6000 |
| ширина 550 мм | 2200 | 3300 | 3740 | 4400 | 4840 | 5280 | 5720 | 6600 |
| ширина 600 мм | 2400 | 3600 | 4080 | 4800 | 5280 | 5760 | 6240 | 7200 |
| ширина 650 мм | 2600 | 3900 | 4420 | 5200 | 5720 | 6240 | 6760 | 7800 |
| ширина 700мм | 2800 | 4200 | 4760 | 5600 | 6160 | 6720 | 7280 | 8400 |
| Ф — профиль 32х28 мм | 280 | 420 | — | 560 | — | — | — | 840 |
| Ф — профиль 50х30 мм | 420 | 630 | — | 840 | — | — | — | 1260 |
| П — профиль | 190 | 285 | — | 380 | — | — | — | 570 |
Белый глянец, мрамор глянец, белый дуб глянец, натуральный дуб глянец, золотой дуб глянец, орех глянец, венге глянец, махагон глянец, антрацит матовый.
| ширина / длина мм | 1000 | 1500 | 1700 | 2000 | 2200 | 2400 | 2600 | 3000 |
| ширина 150 мм | 645 | 967,5 | 1096,5 | 1290 | 1419 | 1548 | 1677 | 1935 |
| ширина 200 мм | 860 | 1290 | 1462 | 1720 | 1892 | 2064 | 2236 | 2580 |
| ширина 250 мм | 1075 | 1612,5 | 1827,5 | 2150 | 2365 | 2580 | 2795 | 3225 |
| ширина 300 мм | 1290 | 1935 | 2193 | 2580 | 2838 | 3096 | 3354 | 3870 |
| ширина 350 мм | 1505 | 2257,5 | 2558,5 | 3010 | 3311 | 3612 | 3913 | 4515 |
| ширина 400 мм | 1720 | 2580 | 2924 | 3440 | 3784 | 4128 | 4472 | 5160 |
| ширина 450 мм | 1935 | 2902,5 | 3289,5 | 3870 | 4257 | 4644 | 5031 | 5805 |
| ширина 500 мм | 2150 | 3255 | 3655 | 4300 | 4730 | 5160 | 5590 | 6450 |
| ширина 550 мм | 2365 | 3547,5 | 4020,5 | 4730 | 5203 | 5676 | 6149 | 7095 |
| ширина 600 мм | 2580 | 3870 | 4386 | 5160 | 5676 | 6192 | 6708 | 7740 |
| ширина 650 мм | 2795 | 4192,5 | 4751,5 | 5590 | 6149 | 6708 | 7267 | 8385 |
| ширина 700 мм | 3010 | 4515 | 5117 | 6020 | 6622 | 7224 | 7826 | 9030 |
| Ф — профиль 32х28 мм | 390 | 585 | — | 780 | — | — | — | 1170 |
| Ф — профиль 50х30 мм | 510 | 765 | — | 1020 | — | — | — | 1530 |
| П — профиль | 270 | 405 | — | 540 | — | — | — | 810 |
Более подробную информацию можно прочитать на сайте производителя Crystallit. Также, Вы можете ознакомиться со всеми образцами предлагаемой продукции и получить квалифицированную консультацию в наших офисах.
Также, Вы можете ознакомиться со всеми образцами предлагаемой продукции и получить квалифицированную консультацию в наших офисах.
ВАЖНО: возможны сколы по периметру (допустимый размер сколов до 1мм),
во избежание недоразумений одновременно с откосами заказывайте стартовые и финишные профили.
Пластиковые откосы для окон в Перми в розницу и оптом: цены
На складе ООО «ПермОкнаСервис» Вы можете купить готовые откосы ПВХ и сэндвич-панели 10 мм листами для отделки окон и дверей, а также стартовый и F-профиль к ним.
Осуществляем доставку и комплектацию.
Преимущества откосов РОССТАР:- Чистый белый цвет. Цвет однотонный во всех партиях.
- Утолщенный пластик. Два варианта — 0,45 и 0,7 мм. У конкурентов-аналогов — 0,2-0,3 мм.
- Высокая прочность пластика на сжатие: 0,27 Мпа при 10% линейной деформации. Подходит даже для оформления арочных окон.

- Равномерное проклеивание слоев путем горячего прессования.
- Высокая теплоизоляция (0,041 Вт/м2К).
- Шумопоглощение звуков улицы.
- Стойкость к солнечным лучам. Сохраняет белый цвет в течении 15-20 лет.
- Практически не поглощают воду по сравнению с гипсокартоном, поэтому на пластиковых откосах реже образуется плесень даже при наличии конденсата.
- Полностью готовы к установке. Легко моются бытовыми моющими средствами.
Цены
Откосы, стартовый (п-образный) и ф-образный профиль
| Размеры, мм | Цена, руб |
| 100*1500 | 101,25 |
| 100*2000 | 144,00 |
| 100*3000 | 216,00 |
| 200*1500 | 202,50 |
| 250*1500 | 253,10 |
| 200*2000 | 288,00 |
| 250*2000 | 360,00 |
| 200*2250 | 324,00 |
| 250*2250 | 405,00 |
| 200*3000 | 432,00 |
| 250*3000 | 540,00 |
| 300*1500 | 303,75 |
| 400*1500 | 405,00 |
| 300*2000 | 432,00 |
| 400*2000 | 576,00 |
| 300*2250 | 486,00 |
| 400*2250 | 648,00 |
| 300*3000 | 648,00 |
| 400*3000 | 864,00 |
| Размеры, мм | Цена, руб |
| 500*1500 | 506,25 |
| 600*1500 | 607,5 |
| 500*2000 | 720,00 |
| 600*2000 | 864,00 |
| 500*2250 | 810,00 |
| 600*2250 | 972,00 |
| 500*3000 | 1080,00 |
| 600*3000 | 1296,00 |
| 750*1500 | 759,40 |
| 1000*1500 | 1012,50 |
| 750*2250 | 1215,00 |
| 1000*2250 | 1620,00 |
| 750*3000 | 1620,00 |
| 1000*3000 | 2160,00 |
| ЛИСТ 1500*3000 | 1640,00 |
| Ваши размеры | дог.
|
| П-профиль (стартовый) | 35,00 |
| F-профиль (уголок) | 45,00 |
| Крепление откоса | 15,00 |
Готовые наборы для отделки откосов
В каждый набор входит:
- Откосы из сэндвич-панелей
- Стартовый профиль — необходим для герметичного крепления откоса к раме
- F-профиль (уголок) — служит для окантовки стыка откоса и стены
| Ширина откосов, мм | Цена, руб |
| До 300 | 1271,25 |
| 300-500 | 1878,75 |
| 500-600 | 2182,50 |
| 600-1000 | 3600,00 |
| Ширина откосов, мм | Цена, руб |
| До 300 | 1513,50 |
| 300-500 | 2242,50 |
| 500-600 | 2607,00 |
| 600-1000 | 4200,00 |
| Ширина откосов, мм | Цена, руб |
| До 300 | 1906,80 |
| 300-500 | 2818,20 |
| 500-600 | 3273,75 |
| 600-1000 | 5400,00 |
Дополнительно понадобится
Подоконники
Крепеж для окон
Пена, герметики, химия
Отливы для окон
Купить пластиковые откосы и сэндвич-панели в розницу и оптом можно на складе по адресу Героев Хасана, 68. Телефон торгового зала (342)243-03-45.
Телефон торгового зала (342)243-03-45.
Посмотреть, как проехать и время работы торгового зала
Посмотреть цены на оконную фурнитуру
Сохранить информацию к себе:
Профиль свободной поверхности – обзор
Перечислите основные допущения уравнений Сен-Венана.
Какова скорость небольшого возмущения в (1) прямоугольном канале, (2) 90° V-образном канале и (3) канале неправильного сечения? (4) Применение: поперечное сечение поймы имеет следующие характеристики: гидравлический диаметр = 5,14 м, максимальная глубина воды = 2,9 м, смоченный периметр = 35 м, ширина по свободной поверхности = 30 м.Вычислите быстроту небольшого возмущения.
Небольшая волна высотой 0,2 м распространяется вниз по течению в горизонтальном канале с начальными условиями течения V = + 0,1 м/с и d = 2,2 м. Вычислите скорость распространения небольшой волны.
В длинном прямоугольном канале достигаются равномерные равновесные условия течения ( W = 12,8 м, с бетонным покрытием, S o = 0,0005).Наблюдаемая глубина воды составляет 1,75 м. Вычислите скорость небольшой моноклинальной волны, распространяющейся вниз по течению. Выполните расчеты, используя коэффициент трения Дарси .
Расход в прямоугольном канале ( W = 3,4 м, облицованный бетоном, S o = 0,0007) составляет 3,1 м 3 9004 условия равномерный поток . Расход резко возрастает до 5,9 м 3 /с. Вычислите скорость моноклинальной волны.За какое время моноклинальная волна пройдет 20 км?
Каково основное определение простой волны? Можно ли применить простую волновую теорию к (1) наклонному каналу без трения, (2) горизонтальному каналу с неровностями, (3) положительному нагону в горизонтальном гладком канале с постоянной глубиной воды и (4) гладкому горизонтальному каналу. канал с изначально ускоряющимся потоком?
канал с изначально ускоряющимся потоком?
Что такое «зона покоя»?
Другим основным применением является река, впадающая в море, и выше по течению степень приливно-отливного воздействия на свободную поверхность. С учетом впадающего в море ручья длина приливов составляет 0,8 м, а продолжительность приливов — 12 ч 25 мин. Начальные условия течения: V = 0,3 м/с, d = 0,4 м, что соответствует отливу. Пренебрегая уклоном дна и сопротивлением течению и начиная с отлива, рассчитайте, насколько вверх по течению поднимется уровень реки через 3 часа после отлива, и предскажите профиль свободной поверхности при t = 3 часа.
Принимая во внимание длинный горизонтальный прямоугольный канал ( W = 4,2 м), работа затвора на одном конце канала вызывает внезапный забор воды, что приводит к отрицательной скорости. В воротах граничные условия для t > 0 таковы: V ( x = 0, t ) = −0,2 м/с. Рассчитайте степень влияния работы затвора в канале при t = 1 час. Начальные условия в канале: V = 0 и d = 1.4 м.
Рассчитайте степень влияния работы затвора в канале при t = 1 час. Начальные условия в канале: V = 0 и d = 1.4 м.
Расход воды в оросительном канале в установившемся режиме ( V = 0,9 м/с, d = 1,65 м). Лоток предполагается гладким и горизонтальным. Поток контролируется выходным затвором. При t = 0 ворота очень медленно поднимаются, и глубина воды перед воротами уменьшается со скоростью 5 см/мин, пока глубина воды не станет 0,85 м. (1) Постройте профиль свободной поверхности при t = 10 мин. (2) Рассчитайте расход на единицу ширины затвора при t = 10 мин.
Прямоугольный канал длиной 200 км ( W = 3,2 м) имеет водохранилище на верхнем конце и ворота на нижнем конце. В начальный момент условия течения в канале равномерны: V = 0,35 м/с, d = 1,05 м. Уровень поверхности воды в водохранилище начинает подниматься со скоростью 0,2 м/ч в течение 6 ч. Рассчитайте условия течения в канале при t = 2 ч. Предположим, что S или = S f = 0.
Рассчитайте условия течения в канале при t = 2 ч. Предположим, что S или = S f = 0.
Воды текут в горизонтальном гладком прямоугольном канале. Начальные условия течения: d = 2,1 м и V = + 0,3 м/с. Скорость потока останавливается внезапным закрытием затвора на нижнем конце канала. Используя аналогию с квазистационарным потоком, рассчитайте новую глубину воды и скорость полностью развитого фронта нагона.
Рассмотрим ту же задачу, что и выше (т. е. горизонтальный гладкий прямоугольный канал, d = 2.1 м и V = 0,3 м/с), но нижний затвор закрывается медленно со скоростью, соответствующей линейному уменьшению расхода от 0,63 м 2 /с до 0 за 15 мин. (1) Прогноз развития фронта нагона. (2) Рассчитать профиль свободной поверхности при t = 1 ч после начала закрытия ворот.
Воды текут по горизонтальному гладкому прямоугольному оросительному каналу. Начальные условия течения: d = 1,1 м и В = +0.35 м/с. Между t = 0 и t = 10 мин нижний затвор медленно поднимается со скоростью, подразумевающей уменьшение глубины воды на 0,05 м/мин. Для t > 10 мин положение ворот поддерживается постоянным. Рассчитайте и начертите профиль свободной поверхности в канале при t = 30 мин. Использовать простую волновую аппроксимацию .
Начальные условия течения: d = 1,1 м и В = +0.35 м/с. Между t = 0 и t = 10 мин нижний затвор медленно поднимается со скоростью, подразумевающей уменьшение глубины воды на 0,05 м/мин. Для t > 10 мин положение ворот поддерживается постоянным. Рассчитайте и начертите профиль свободной поверхности в канале при t = 30 мин. Использовать простую волновую аппроксимацию .
Передний заливной канал шириной 5 м снабжает водовод турбиной Пельтона. Начальные условия в канале: V = 0 и d = 2.5 м. (1) Турбина внезапно начинает работать со скоростью 6 м 3 /с. Предсказать глубину воды в нижнем конце канала форбухты. (2) Каков максимальный расход, который может обеспечить передний канал? Использовать простую волновую теорию .
Напишите кинематическое волновое уравнение для широкого прямоугольного русла с учетом скорости потока, уклона дна и глубины воды. Какова скорость кинематической волны? Предсказывает ли кинематическая маршрутизация волн оседание?
Какова скорость кинематической волны? Предсказывает ли кинематическая маршрутизация волн оседание?
Широкий канал имеет уклон дна S o = 0,0003 и дно канала имеет эквивалентную высоту шероховатости 25 мм. Начальная глубина потока составляет 2,3 м, при этом достигается равномерный равновесный режим течения. Глубина воды резко увеличивается до 2,4 м в верхнем конце канала. Вычислите скорость диффузионной волны и коэффициент диффузии.
Прямоугольный канал шириной 8 м (бетонная облицовка) работает в условиях однородного равновесного потока при расходе 18 м 3 /с, что приводит к 1.Глубина воды 8 м. В верхнем конце расход внезапно увеличивается до 18,8 м 3 /с. Рассчитайте скорость потока в канале через 1 ч в точке x = 15 км. Использовать диффузионную маршрутизацию .
Словарь CWFF по фортификации: Словарь: профиль, парапет и ров
Профиль – это поперечное сечение парапета и рва, снятое
вдоль линии, перпендикулярной общему направлению внутреннего гребня
парапета или с внутренней стороны парапета с внешней стороны
работа. Он показывает, в основном, вертикальный срез работы и графически
описывает высоту, толщину и общее расположение различных
элементы работы. Профили всех основных полевых работ включали два основных
элементы: парапет и ров. Парапет служил защитой
масса земли, которая защищала внутреннюю часть работы от вражеского огня и,
в сочетании со рвом служил главным препятствием для войск противника
попытка проникнуть на работу во время штурма. Канава была и препятствием
и основной источник почвы, используемой для строительства парапета.
Он показывает, в основном, вертикальный срез работы и графически
описывает высоту, толщину и общее расположение различных
элементы работы. Профили всех основных полевых работ включали два основных
элементы: парапет и ров. Парапет служил защитой
масса земли, которая защищала внутреннюю часть работы от вражеского огня и,
в сочетании со рвом служил главным препятствием для войск противника
попытка проникнуть на работу во время штурма. Канава была и препятствием
и основной источник почвы, используемой для строительства парапета.
Хорошо построенный парапет и ров состояли из различные возвышения и поверхности специальной формы, которые были устроены для улучшения оборонительные качества работы, позволяют гарнизону подметать землю перед работой с его огнем, и в целом повысить стабильность и выносливость конструкции. Профиль основная работа обычно состоял из десяти первоэлементов; взято в порядке из салона к внешности эти элементы были:
A. Земельная площадь или пространство, окруженное укреплением или
сразу к задней части парапета, который обычно был выровнен до
равнина сайта.
B. Банкетный склон, который позволял войскам стоять на парапете. удобный доступ к банкетке;
C. Поступь банкета, где войска у парапета стояли, чтобы доставить их огонь;
D. Внутренний склон высотой примерно 4,5 фута. которая образовывала внутреннюю сторону парапета и обычно облицовывалась сохранить почву, из которой состоит парапет, на неестественно крутом склоне;
E. Верхний склон, образующий верхнюю поверхность парапета. и был слегка наклонен к внешней стороне работы, чтобы позволить войскам направьте свои винтовки или мушкеты вниз, чтобы осмотреть землю прямо перед собой рва;
Ф.Внешний уклон, которому обычно позволяли принимать естественный вид. уклон рыхлого грунта и поверхность, необходимая для поглощения воздействие огня большей части противника, направленного на работу;
G. Берма, ровный участок, оставшийся между внешним склоном и рвом, который предназначался для уменьшения давления веса парапета на внутренний уклон канавы для предотвращения размывания парапета в канаву;
H. Контрэскарп рва был внутренней стеной
канаву и обычно имел уклон, который позволял ему выдерживать вес
парапет без обрушения;
Контрэскарп рва был внутренней стеной
канаву и обычно имел уклон, который позволял ему выдерживать вес
парапет без обрушения;
Я.Дно рва;
J. Уступ, образующий внешнюю стену рва;
К. Гласис представлял собой приподнятую насыпь земли перед рвом. с длинным пологим склоном впереди, который должен был увеличить высоту земли за пределами работы и не дать вражеским войскам возможности проскользнуть под огнем, поставленным с бруствера.
Углы, при которых две поверхности пересекаются в выступающем (внешний) угол назывался «гребнем»; углы, образующие повторно входящие (внутренние) углом называли «подножие» наиболее приподнятых скрещивающихся поверхностей.Линия, где внутренний откос пересекает верхний откос, например, назывался «гребень внутреннего склона» или просто «внутренний гребень». То линия, где внутренний уклон приходился на ступени банкетки, называлась «подножие внутреннего склона».
Стандарт Пропорции
Основные полевые работы, построенные во время Гражданской войны в США. Война обычно следовала общепринятым методам, которые были выработаны путем
предыдущие два столетия. Стандартные пропорции были в основном выражением
народной мудрости относительно устойчивости защитной насыпи
и структурные характеристики, необходимые для того, чтобы насыпь служила
как укрытие, препятствие и эффективная площадка для оборонительного огня.Каждый элемент
основного парапета для полевых работ имел четкую функцию и был пропорционален
и создан для выполнения этой функции. Эти пропорции могут быть изменены как
необходимы для получения определенного эффекта или изменены ограничениями, налагаемыми
по времени, трудам и материалам. Стандартные пропорции были руководством для производства
эффективный парапет, неизменные и универсально применимые законы
природа; обязанностью инженера и других офицеров было творчески применить
собственный здравый смысл и опыт при адаптации стандартов к конкретным
ситуации.
Война обычно следовала общепринятым методам, которые были выработаны путем
предыдущие два столетия. Стандартные пропорции были в основном выражением
народной мудрости относительно устойчивости защитной насыпи
и структурные характеристики, необходимые для того, чтобы насыпь служила
как укрытие, препятствие и эффективная площадка для оборонительного огня.Каждый элемент
основного парапета для полевых работ имел четкую функцию и был пропорционален
и создан для выполнения этой функции. Эти пропорции могут быть изменены как
необходимы для получения определенного эффекта или изменены ограничениями, налагаемыми
по времени, трудам и материалам. Стандартные пропорции были руководством для производства
эффективный парапет, неизменные и универсально применимые законы
природа; обязанностью инженера и других офицеров было творчески применить
собственный здравый смысл и опыт при адаптации стандартов к конкретным
ситуации.
Гласис (К)
Гласис состоял из холма с очень пологим уклоном, который простирался
наружу от гребня контрэскарпа. Гласис был включен в состав
общий профиль полевых работ, когда разница в высоте между
внутренний гребень парапета в сочетании со степенью уклона с учетом
верхний гребень и высота гребня контрэскарпа рва
не допустить, чтобы огонь стрелкового оружия гарнизона достиг точки не менее 2 футов
над гребнем контрэскарпа.Гласис поднял уровень земли
непосредственно перед работой и гарантировал, что атакующая группировка войск
не мог проскользнуть в ров, не получив предварительно огня гарнизона
вблизи. Это также имело то преимущество, что заставило атакующую группу
войск продвигаться по склону, чтобы добраться до рва. не было фиксированных
размеры гласиса как элемента профиля полевого укрепления;
общее правило указывало, что она должна быть достаточно высокой для ведения огня
от парапета проходить не более чем в двух футах над его гребнем возле гребня
контрэскарпа.Земля для строительства гласиса обычно добывалась
путем расширения или углубления канавы.
Гласис был включен в состав
общий профиль полевых работ, когда разница в высоте между
внутренний гребень парапета в сочетании со степенью уклона с учетом
верхний гребень и высота гребня контрэскарпа рва
не допустить, чтобы огонь стрелкового оружия гарнизона достиг точки не менее 2 футов
над гребнем контрэскарпа.Гласис поднял уровень земли
непосредственно перед работой и гарантировал, что атакующая группировка войск
не мог проскользнуть в ров, не получив предварительно огня гарнизона
вблизи. Это также имело то преимущество, что заставило атакующую группу
войск продвигаться по склону, чтобы добраться до рва. не было фиксированных
размеры гласиса как элемента профиля полевого укрепления;
общее правило указывало, что она должна быть достаточно высокой для ведения огня
от парапета проходить не более чем в двух футах над его гребнем возле гребня
контрэскарпа.Земля для строительства гласиса обычно добывалась
путем расширения или углубления канавы.
То Канава (H, I, J)
Хотя объем грунта, необходимый для строительства
парапет конкретного же можно было точно рассчитать по большей части
была оценена ширина и глубина рва, необходимые для производства достаточного количества почвы. Наиболее распространенный метод состоял в том, чтобы предположить глубину рва и разделить ее
по сумме площади поверхности профиля парапета. Поскольку
ров был задуман как препятствие, минимально допустимым считалось 6 футов
глубина и 12 футов были минимальной шириной.Если это произвело слишком много почвы,
дополнительный был преобразован в гласис. Уступ рва обычно давался
основание, равное 2/3 естественного угла грунта (то есть 2/3
глубина рва), а контрэскарпу дали основание, равное 1/2
основание уступа. Ров шириной 16 футов наверху и глубиной 10 футов в нормальном состоянии.
почвы, потребуется основание в 6 футов для уступа (примерно 1/3
10) и основание в 3 фута для контрэскарпа (1/2 из 6), которое оставит
ширина дна канавы 7 футов.
Наиболее распространенный метод состоял в том, чтобы предположить глубину рва и разделить ее
по сумме площади поверхности профиля парапета. Поскольку
ров был задуман как препятствие, минимально допустимым считалось 6 футов
глубина и 12 футов были минимальной шириной.Если это произвело слишком много почвы,
дополнительный был преобразован в гласис. Уступ рва обычно давался
основание, равное 2/3 естественного угла грунта (то есть 2/3
глубина рва), а контрэскарпу дали основание, равное 1/2
основание уступа. Ров шириной 16 футов наверху и глубиной 10 футов в нормальном состоянии.
почвы, потребуется основание в 6 футов для уступа (примерно 1/3
10) и основание в 3 фута для контрэскарпа (1/2 из 6), которое оставит
ширина дна канавы 7 футов.
Берм (G)
Обычно считается дефектом полевых работ, бермой
часто было необходимо, чтобы разгрузить эскарп от веса
парапет. Его длина была пропорциональна прочности почвы.
В твердом грунте, способном выдержать нагрузку парапета, бермы могли находиться где угодно. шириной от 1 до 2 футов, в болотистой или очень легкой почве, которая имеет тенденцию к смещению
легко под бременем он может быть до 6 футов в ширину. Так как берма обычно
уровне он собирал дождевую воду, стекающую с парапета, и имел тенденцию к эрозии.
быстро; как только он начал ухудшаться, он имел тенденцию носить гребень
спрыгните вниз и начните более или менее медленный процесс заполнения канавы.Эта проблема иногда решалась в полупостоянных укреплениях путем разрезания
от бермы и соединения внешнего склона с уступом и
они падают под естественным углом почвы. Это считалось дефектом, потому что
это давало атакующим войскам точку опоры, где они могли отдохнуть
через мгновение после подъема по уступу перед восхождением на верхний склон. За
по этой причине берма должна была быть не менее чем на шесть футов ниже внутреннего гребня
чтобы атакующие войска не могли стоять на берме и вести огонь
в работу.
шириной от 1 до 2 футов, в болотистой или очень легкой почве, которая имеет тенденцию к смещению
легко под бременем он может быть до 6 футов в ширину. Так как берма обычно
уровне он собирал дождевую воду, стекающую с парапета, и имел тенденцию к эрозии.
быстро; как только он начал ухудшаться, он имел тенденцию носить гребень
спрыгните вниз и начните более или менее медленный процесс заполнения канавы.Эта проблема иногда решалась в полупостоянных укреплениях путем разрезания
от бермы и соединения внешнего склона с уступом и
они падают под естественным углом почвы. Это считалось дефектом, потому что
это давало атакующим войскам точку опоры, где они могли отдохнуть
через мгновение после подъема по уступу перед восхождением на верхний склон. За
по этой причине берма должна была быть не менее чем на шесть футов ниже внутреннего гребня
чтобы атакующие войска не могли стоять на берме и вести огонь
в работу.
Внешний уклон (F)
Внешний склон был сделан так, что почва рыхлая. брошенный в кучу естественно предполагал бы. Это был угол 45 градусов
поэтому основание внешнего склона обычно равнялось высоте внешнего
герб Ожидалось, что эта поверхность примет на себя большую часть направленного огня противника.
на полевых работах. Его естественный угол позволял слагающей его почве быть
подбрасывается в воздух от удара и выстрела и разрыва снарядов и падает
обратно на склон, частично восстанавливая первоначальный урон и увеличивая
период времени, необходимый для обрушения парапета и раскрытия интерьера
работы под огонь противника.Склон также имел то преимущество, что способствовал
хороший дренаж за счет быстрого, но равномерного перемещения стока через берму и
в канаву. Посев или задернивание были необходимы для надлежащего обслуживания
внешнего склона полевых работ, которые должны были стоять в течение длительного
период времени.
брошенный в кучу естественно предполагал бы. Это был угол 45 градусов
поэтому основание внешнего склона обычно равнялось высоте внешнего
герб Ожидалось, что эта поверхность примет на себя большую часть направленного огня противника.
на полевых работах. Его естественный угол позволял слагающей его почве быть
подбрасывается в воздух от удара и выстрела и разрыва снарядов и падает
обратно на склон, частично восстанавливая первоначальный урон и увеличивая
период времени, необходимый для обрушения парапета и раскрытия интерьера
работы под огонь противника.Склон также имел то преимущество, что способствовал
хороший дренаж за счет быстрого, но равномерного перемещения стока через берму и
в канаву. Посев или задернивание были необходимы для надлежащего обслуживания
внешнего склона полевых работ, которые должны были стоять в течение длительного
период времени.
Верхний склон (E)
Верхний склон был наклонен вниз от внутренней части
гребень, позволяющий солдатам, стреляющим с парапета, достаточно нажимать на свои мушкеты
стрелять не выше, чем на три фута выше и поперек гребня контрэскарпа. Наклон может быть равен от 1/4 до 1/6 основания верхнего склона.
Превосходный склон с основанием шириной 12 футов и уклоном в 1/4 его основания будет
быть на 3 фута ниже на гребне внешнего склона, чем на гребне
внутреннего склона. Наклоны более 1/4 были бы слишком слабыми, чтобы предотвратить
огонь противника от пробития бруствера и проникновения вглубь
полевых работ. Склоны менее 1/6 были бы слишком пологими, чтобы войска могли
стрелять вниз с бруствера. Верхний наклон определяет толщину
бруствера и должен был поглощать твердые выстрелы и снаряды, пробивающие
в массу парапета, не разрушаясь слишком быстро.Его стабильность
зависело от способности облицовки внутреннего склона удерживать
масса парапета под относительно острым углом и на грузоподъемность
внешний уклон, чтобы противостоять эрозионному воздействию погоды и поглощать
воздействие цельных дробовых и разрывных снарядов без разрушения и
падение в канаву. Склон также позволял стекать дождевой воде.
поверхность и наружу.
Наклон может быть равен от 1/4 до 1/6 основания верхнего склона.
Превосходный склон с основанием шириной 12 футов и уклоном в 1/4 его основания будет
быть на 3 фута ниже на гребне внешнего склона, чем на гребне
внутреннего склона. Наклоны более 1/4 были бы слишком слабыми, чтобы предотвратить
огонь противника от пробития бруствера и проникновения вглубь
полевых работ. Склоны менее 1/6 были бы слишком пологими, чтобы войска могли
стрелять вниз с бруствера. Верхний наклон определяет толщину
бруствера и должен был поглощать твердые выстрелы и снаряды, пробивающие
в массу парапета, не разрушаясь слишком быстро.Его стабильность
зависело от способности облицовки внутреннего склона удерживать
масса парапета под относительно острым углом и на грузоподъемность
внешний уклон, чтобы противостоять эрозионному воздействию погоды и поглощать
воздействие цельных дробовых и разрывных снарядов без разрушения и
падение в канаву. Склон также позволял стекать дождевой воде.
поверхность и наружу.
Внутренний уклон (D)
Внутренний уклон получил горизонтальное основание, равное
от 1/3 до 1/4 его вертикальной высоты, чтобы войска могли наклоняться вперед для ведения огня
над верхним склоном. Из-за резкого наклона необходимо допустить
войска стоять достаточно близко к верхнему склону, чтобы вести эффективный огонь,
внутренний склон должен был поддерживаться облицовкой. Сильная облицовка была
необходимые для работ, которые должны были сохранить свои защитные качества
дольше нескольких дней или недель; все ограждения, как правило, рушились под
давление, оказываемое весом массы парапета и необходимое
более-менее постоянное обслуживание и ремонт. Прочность облицовки
материал тоже был важен.Дробь и снаряд проникают внутрь и насквозь
масса парапета могла быть остановлена прочной облицовкой; это было
особенно важно при полевых работах, подвергающихся длительной бомбардировке.
Из-за резкого наклона необходимо допустить
войска стоять достаточно близко к верхнему склону, чтобы вести эффективный огонь,
внутренний склон должен был поддерживаться облицовкой. Сильная облицовка была
необходимые для работ, которые должны были сохранить свои защитные качества
дольше нескольких дней или недель; все ограждения, как правило, рушились под
давление, оказываемое весом массы парапета и необходимое
более-менее постоянное обслуживание и ремонт. Прочность облицовки
материал тоже был важен.Дробь и снаряд проникают внутрь и насквозь
масса парапета могла быть остановлена прочной облицовкой; это было
особенно важно при полевых работах, подвергающихся длительной бомбардировке.
Поступь Банкетки (C)
Шаг банкетки обычно составлял от 4 до 4,5 футов.
ниже гребня внутреннего склона, так что даже самые низкорослые мужчины в
ряды могли поднять свои мушкеты достаточно высоко, чтобы стрелять по более высокому склону.
Его ширина зависела от количества шеренг, которые должны были образоваться в войсках при комплектовании. парапет.Одной шеренге разрешалась банкетка шириной 2 фута, 2 или 3 шеренги —
есть банкетка шириной 4 фута. Для обеспечения хорошего дренажа банкетка была
обычно имеют очень небольшой наклон к задней части, чтобы сток мог течь
легко вниз по склону банкетки и на terreplein. Сильная защита
частично зависело от банкетки, которая была относительно свободна от препятствий,
легко передвигаться и служила прочной и надежной базой для подкладки войск
бруствер, на котором можно стоять во время боя с атакующими войсками.Если
сделаны слишком узкими или наклонены слишком радикально, войска стоят на банкете
будет трудно поддерживать равновесие и оставаться на месте
стрелять и перезаряжать свои винтовки или мушкеты.
парапет.Одной шеренге разрешалась банкетка шириной 2 фута, 2 или 3 шеренги —
есть банкетка шириной 4 фута. Для обеспечения хорошего дренажа банкетка была
обычно имеют очень небольшой наклон к задней части, чтобы сток мог течь
легко вниз по склону банкетки и на terreplein. Сильная защита
частично зависело от банкетки, которая была относительно свободна от препятствий,
легко передвигаться и служила прочной и надежной базой для подкладки войск
бруствер, на котором можно стоять во время боя с атакующими войсками.Если
сделаны слишком узкими или наклонены слишком радикально, войска стоят на банкете
будет трудно поддерживать равновесие и оставаться на месте
стрелять и перезаряжать свои винтовки или мушкеты.
То Банкетный склон (B)
Наклон банкетки задавался основанием равным
в два раза выше высоты проступи банкетки. Учитывая внутренний герб
8 футов над уровнем земли, ступени банкетки
быть примерно на 4 фута 6 дюймов ниже внутреннего гребня и на 3 фута 6 дюймов выше
уровень земли. Тогда наклон банкетки будет
основание 7 футов. Когда полное основание банкетного склона теснило салон
площадь полевой работы слишком велика, ее можно разрезать на ступени шириной 12 дюймов.
и девять дюймов в высоту. Легкий доступ к проступи банкетки был чрезвычайно важен,
особенно когда гарнизон был неожиданно призван занять парапет и
приходилось спешить на позицию в темноте или полумраке рассвета.
Тогда наклон банкетки будет
основание 7 футов. Когда полное основание банкетного склона теснило салон
площадь полевой работы слишком велика, ее можно разрезать на ступени шириной 12 дюймов.
и девять дюймов в высоту. Легкий доступ к проступи банкетки был чрезвычайно важен,
особенно когда гарнизон был неожиданно призван занять парапет и
приходилось спешить на позицию в темноте или полумраке рассвета.
[Эта страница изначально отображалась как страница с основной информацией на старом веб-сайте полевых укреплений Гражданской войны.]
Ориентация профиля и анализ устойчивости откосов
В данной статье представлен анализ устойчивости откосов грунта с использованием наземного лазерного сканера, оптимизации роя частиц и метода силового равновесия. Цель этого исследования заключалась в том, чтобы продемонстрировать, что склон необходимо анализировать во многих различных направлениях, чтобы окончательно оценить его устойчивость, а не использовать только один профиль поперечного сечения для представления всего склона. Для достижения этой цели данное исследование иллюстрирует, как алгоритм оптимизации скопления частиц может быть успешно включен в анализ с помощью программного обеспечения для анализа устойчивости откосов STABL.В этом исследовании сравниваются результаты, полученные с результатами предыдущих исследований, и делаются важные наблюдения.
Для достижения этой цели данное исследование иллюстрирует, как алгоритм оптимизации скопления частиц может быть успешно включен в анализ с помощью программного обеспечения для анализа устойчивости откосов STABL.В этом исследовании сравниваются результаты, полученные с результатами предыдущих исследований, и делаются важные наблюдения.
1. Введение
Оползни, вызванные дождем, являются обычным явлением в субтропическом Тайване, где часто случаются сильные дожди из-за тайфунов. Предметом исследования являются направление и механизм движения неустойчивого откоса. Традиционно состояние равновесия земляного откоса оценивается его коэффициентом безопасности (FS), который определяется как отношение общей силы сопротивления к общей движущей силе, как показано в следующем уравнении: где — общие силы сопротивления и — суммарные движущие силы.
Фактический расчет FS — это процесс проб и ошибок, поскольку он зависит от выбора поверхности скольжения из множества возможных вариантов. Обычно тестируется фиксированное количество поверхностей скольжения, и наиболее критической поверхностью скольжения является та, которая дает наименьший FS. Ряд исследований предполагает, что включение в вычисления алгоритмов искусственного интеллекта, таких как оптимизация роя частиц (PSO), может улучшить эту практику. PSO — это недорогой в вычислительном отношении алгоритм, разработанный Кеннеди и Эберхартом [1, 2], который уходит корнями как в искусственную жизнь, так и в эволюционные вычисления.Ниже приводится одна из его самых оригинальных форм (с изменением символов): где настоящее местоположение (инициализируется случайным образом), скорость частицы (инициализируется случайным образом), вес инерции (добавлен к исходной формуле PSO в [3]), есть p_increment (= 2, чтобы пролететь над целью в половине случаев [1]), является случайным числом от 0 до 1, является g_increment (= 2, чтобы пролетать над целью в половине случаев [1]), является случайным числом от 0 до 1, лично лучшая позиция, и это лучшая позиция в мире.
Обычно тестируется фиксированное количество поверхностей скольжения, и наиболее критической поверхностью скольжения является та, которая дает наименьший FS. Ряд исследований предполагает, что включение в вычисления алгоритмов искусственного интеллекта, таких как оптимизация роя частиц (PSO), может улучшить эту практику. PSO — это недорогой в вычислительном отношении алгоритм, разработанный Кеннеди и Эберхартом [1, 2], который уходит корнями как в искусственную жизнь, так и в эволюционные вычисления.Ниже приводится одна из его самых оригинальных форм (с изменением символов): где настоящее местоположение (инициализируется случайным образом), скорость частицы (инициализируется случайным образом), вес инерции (добавлен к исходной формуле PSO в [3]), есть p_increment (= 2, чтобы пролететь над целью в половине случаев [1]), является случайным числом от 0 до 1, является g_increment (= 2, чтобы пролетать над целью в половине случаев [1]), является случайным числом от 0 до 1, лично лучшая позиция, и это лучшая позиция в мире.
В этой статье представлен анализ устойчивости склона около Тайбэя с использованием PSO и FS.Склон был просканирован лазером для получения точных топографических профилей и проанализирован от 0° до 359° с интервалом в 1°. Поскольку найти идеальное место для изучения оползней очень сложно, и на выполнение одного исследования могут уйти годы, авторы считают, что эта работа представляет собой ценный пример для инженеров, заинтересованных в многонаправленном анализе оползней с использованием метода роевого интеллекта.
2. Метод исследования
Это исследование проводилось недалеко от пешеходной тропы Хоушаньюэ, примерно в 25 км от центра города Тайбэй.В целом на территории произошла серия оползней после нескольких тайфунов в течение нескольких лет. Объектом исследования стал один из склонов, пострадавших от оползней. Аэрофотоснимок на рис. 1(а) показывает место исследования. Сканирование склона (отмечено красным квадратом) и непосредственной области с помощью наземного лазерного сканера позволило получить модель облака точек, показанную на рисунке 1(b).
После создания модели облака точек растительность была удалена цифровым способом (с помощью программного инструмента RiScan Pro), чтобы выявить голые почвы.Затем через склон были сделаны воображаемые вертикальные разрезы для создания профилей поперечного сечения для последующего анализа устойчивости склона, как показано на рисунке 1(c). Было сделано три вида разрезов. Сначала было сделано 45 параллельных разрезов с севера на юг (на расстоянии 1 м друг от друга) для изучения изменения FS с профилями, как показано на рисунке 1 (d). Затем было сделано 19 вертикальных поперечных разрезов, ориентированных под углом 45° к северному направлению, как показано на рисунке 1(e), для изучения изменения FS с профилями. Результаты этих двух наборов анализа были представлены на двух конференциях [4, 5].Это исследование сосредоточено на последнем типе профиля разреза, который состоял из непараллельных разрезов в направлениях от 0° до 359°, как показано на рисунке 1(f). Следовательно, это исследование рассмотрело и сравнило 360 возможных профилей.
Исследование проводилось в соответствии с этапами, показанными на рис. 2. После загрузки данных облака точек и цветных панорамных фотографий склона с лазерного сканера на настольный компьютер необработанные данные облака точек и панорамные фотографии были зарегистрированы вместе для создания Модель облака точек склона.Склон был срезан от самой высокой точки склона (нижний левый угол склона), а срезы были развернуты веером от 0° до 359°. Сгенерированные таким образом вертикальные профили поперечного сечения были введены в стандартное программное обеспечение для анализа устойчивости откосов STABL (двухмерная программа анализа предельного равновесия, разработанная Университетом Пердью) для расчета FS каждого профиля. Пользовательские коды Fortran, аналогичные [6], использовались для чтения выходных файлов STABL и автоматического изменения параметров анализа на основе алгоритма PSO.Затем компьютер генерировал новые входные файлы и снова вводил их в программу STABL. Процесс продолжался до тех пор, пока значения FS не сошлись.
2.1. Упрощенный метод Бишопа
Программа STABL использует метод срезов для анализа устойчивости откосов [7]. Для метода срезов (как показано на рисунке 3) склон сначала разбивается на множество вертикальных срезов и анализируется равновесие сил и равновесие моментов. Поскольку переменных было больше, чем уравнений равновесия, мы сделали предположения, чтобы уменьшить количество переменных и решить для FS.Различные методы срезов имели разные предположения. Для круговых поверхностей разрушения (тип поверхностей разрушения, используемый в этом исследовании) на склоне грунта STABL рекомендовала упрощенный/модифицированный метод Бишопа (с использованием команды CIRCL2) для достижения как скорости, так и точности [8]. На рис. 3 показана схема репрезентативного среза и сил, действующих на срез упрощенного метода Бишопа. Было четыре предположения о равновесии: (1) полное равновесие момента было удовлетворено. (2) равновесие момента среза не было удовлетворено. (3) Равновесие вертикальных сил между слоями было удовлетворено. (4) Равновесие горизонтальных сил между слоями не было удовлетворено. Другими словами, упрощенный метод Бишопа предполагал, что силы между слоями были горизонтальными и что не было сил сдвига. Ниже представлена ФС по (1) и рис. 3 для упрощенного метода Бишопа [9, 10] (с изменением обозначений): где – сцепление грунта, – угол трения, – ширина слоя грунта, – ширина слоя грунта. вдоль поверхности скольжения, — вес слоя почвы, — сила сопротивления слоя почвы, — нормальная сила слоя почвы, — сила воды, — поровое давление воды, — угол наклона слоя почвы, — сила между слоями.
(3) Равновесие вертикальных сил между слоями было удовлетворено. (4) Равновесие горизонтальных сил между слоями не было удовлетворено. Другими словами, упрощенный метод Бишопа предполагал, что силы между слоями были горизонтальными и что не было сил сдвига. Ниже представлена ФС по (1) и рис. 3 для упрощенного метода Бишопа [9, 10] (с изменением обозначений): где – сцепление грунта, – угол трения, – ширина слоя грунта, – ширина слоя грунта. вдоль поверхности скольжения, — вес слоя почвы, — сила сопротивления слоя почвы, — нормальная сила слоя почвы, — сила воды, — поровое давление воды, — угол наклона слоя почвы, — сила между слоями.
2.2. Сценарии с использованием PSO
Уравнения (3) показывают, что решение FS представляет собой очень сложную функцию, не имеющую прямых решений. Поскольку FS появляется в обеих частях уравнений, решение FS требует итеративного подхода. Подстановка исходной предполагаемой FS в (3) необходима для вычисления новой FS. Если две ФС различны, то исходная ФС отбрасывается. Уравнения (3) используют новый FS для вычисления другого значения FS. Процесс будет продолжаться до тех пор, пока и предполагаемая, и полученная ФС окончательно не сойдутся к одному и тому же значению.Основываясь на предыдущем опыте, авторы нашли способ делегировать эту вычислительную задачу программе STABL и использовать программу STABL в качестве вычислительной машины [6]. PSO из-за своей простоты идеально подходил для этой конкретной цели. Ему не нужно было ни знать внутреннюю работу STABL, ни знать, как решать FS с помощью упрощенного метода Бишопа. Все, что требовалось от PSO, — это контролировать выполнение STABL и настраивать параметры во входных файлах в соответствии с результатами, возвращаемыми программой STABL.В некотором смысле PSO функционировал и действовал подобно сценарию, и авторы выбрали PSO для этого исследования из-за его относительно простой реализации и простого управления.
Уравнения (3) используют новый FS для вычисления другого значения FS. Процесс будет продолжаться до тех пор, пока и предполагаемая, и полученная ФС окончательно не сойдутся к одному и тому же значению.Основываясь на предыдущем опыте, авторы нашли способ делегировать эту вычислительную задачу программе STABL и использовать программу STABL в качестве вычислительной машины [6]. PSO из-за своей простоты идеально подходил для этой конкретной цели. Ему не нужно было ни знать внутреннюю работу STABL, ни знать, как решать FS с помощью упрощенного метода Бишопа. Все, что требовалось от PSO, — это контролировать выполнение STABL и настраивать параметры во входных файлах в соответствии с результатами, возвращаемыми программой STABL.В некотором смысле PSO функционировал и действовал подобно сценарию, и авторы выбрали PSO для этого исследования из-за его относительно простой реализации и простого управления.
3. Компьютерный анализ
Компьютерный анализ в этом исследовании выполнялся следующим образом: (1) Создайте модель облака точек с помощью RiScan Pro и необработанных данных сканирования. (2) Отфильтруйте растительность и выявите голую почву под ней. (3) Используйте. метод триангулированной нерегулярной сети (TIN) для создания представления земной поверхности склона (голых почв).(4) Выберите зону/область склона для анализа. (5) Выберите самую высокую точку склона. (6) Используя самую высокую точку в качестве начала координат, используйте воображаемую вертикальную плоскость, чтобы рассечь склон от 0° до 359°. ° с интервалом в 1°. Это делается программно. (7) Разрезы будут пересекаться с поверхностями TIN и генерировать следы профилей поперечного сечения склона. Это также делается программно. (8) Поскольку нижняя левая часть местности (юго-западная часть области на рис. 1) образует холм, скатывание склона в холм кинематически невозможно.Следовательно, было создано только 180 профилей из 360 возможных направлений. (9) Создайте входные файлы для программы STABL, используя профили поперечного сечения и параметры грунта из близлежащего бурового теста. (10) Программа STABL, вызываемая программой-скриптом.
(2) Отфильтруйте растительность и выявите голую почву под ней. (3) Используйте. метод триангулированной нерегулярной сети (TIN) для создания представления земной поверхности склона (голых почв).(4) Выберите зону/область склона для анализа. (5) Выберите самую высокую точку склона. (6) Используя самую высокую точку в качестве начала координат, используйте воображаемую вертикальную плоскость, чтобы рассечь склон от 0° до 359°. ° с интервалом в 1°. Это делается программно. (7) Разрезы будут пересекаться с поверхностями TIN и генерировать следы профилей поперечного сечения склона. Это также делается программно. (8) Поскольку нижняя левая часть местности (юго-западная часть области на рис. 1) образует холм, скатывание склона в холм кинематически невозможно.Следовательно, было создано только 180 профилей из 360 возможных направлений. (9) Создайте входные файлы для программы STABL, используя профили поперечного сечения и параметры грунта из близлежащего бурового теста. (10) Программа STABL, вызываемая программой-скриптом. обрабатывает входные файлы по отдельности. (11) Программа сценария считывает выходные файлы (в частности, значения FS в выходных файлах) из программы STABL. (12) Программа STABLE обрабатывает следующий набор входных файлов на основе предыдущих значений FS. и алгоритм PSO, который генерирует второй набор выходных файлов.Процесс продолжается с последовательными наборами входных файлов. (13) В сценарии PSO использовались следующие параметры: , , , и количество частиц = 30. Количество итераций, необходимых для сходимости для разных профилей, варьируется от 1 до 135, в среднем 14,5 раз. (14) Программа сценария останавливается, когда значения FS сходятся. Программа STABL выбирает случайные поверхности скольжения из указанных левого и правого горизонтальных диапазонов (как показано на рисунке 4). Поскольку диапазоны обычно были слишком широкими для формирования наилучшей поверхности скольжения и соответствующей минимальной FS, необходимо было одновременно регулировать размеры левого и правого диапазонов.
обрабатывает входные файлы по отдельности. (11) Программа сценария считывает выходные файлы (в частности, значения FS в выходных файлах) из программы STABL. (12) Программа STABLE обрабатывает следующий набор входных файлов на основе предыдущих значений FS. и алгоритм PSO, который генерирует второй набор выходных файлов.Процесс продолжается с последовательными наборами входных файлов. (13) В сценарии PSO использовались следующие параметры: , , , и количество частиц = 30. Количество итераций, необходимых для сходимости для разных профилей, варьируется от 1 до 135, в среднем 14,5 раз. (14) Программа сценария останавливается, когда значения FS сходятся. Программа STABL выбирает случайные поверхности скольжения из указанных левого и правого горизонтальных диапазонов (как показано на рисунке 4). Поскольку диапазоны обычно были слишком широкими для формирования наилучшей поверхности скольжения и соответствующей минимальной FS, необходимо было одновременно регулировать размеры левого и правого диапазонов. PSO оптимизирует процесс, сопоставляя два диапазона с новым пространством. Координата нового пространства представляет собой левую границу левого диапазона, а координата представляет собой левую границу правого диапазона. Чтобы исследовать как можно больше скользящих поверхностей, оба диапазона и были установлены равными 16 м, как показано на рисунке 4. Пространство 16 на 16 было определено как пространство поиска, которое было воображаемым пространством, созданным исключительно для PSO. формулировка. Стоит отметить, что внутри этого воображаемого пространства функция объекта (FS) не является явной непрерывной функцией.Скорее, STABL необходимо вычислить значение FS, используя (3), используя итеративный подход. Также обратите внимание, что STABL требует минимальной ширины 0,1 м для работы как левого, так и правого диапазонов. Следовательно, решение в новом пространстве фактически означает левый диапазон и правый диапазон . Это небольшое ограничение обычно не мешает выполнению программы PSO и STABL.
PSO оптимизирует процесс, сопоставляя два диапазона с новым пространством. Координата нового пространства представляет собой левую границу левого диапазона, а координата представляет собой левую границу правого диапазона. Чтобы исследовать как можно больше скользящих поверхностей, оба диапазона и были установлены равными 16 м, как показано на рисунке 4. Пространство 16 на 16 было определено как пространство поиска, которое было воображаемым пространством, созданным исключительно для PSO. формулировка. Стоит отметить, что внутри этого воображаемого пространства функция объекта (FS) не является явной непрерывной функцией.Скорее, STABL необходимо вычислить значение FS, используя (3), используя итеративный подход. Также обратите внимание, что STABL требует минимальной ширины 0,1 м для работы как левого, так и правого диапазонов. Следовательно, решение в новом пространстве фактически означает левый диапазон и правый диапазон . Это небольшое ограничение обычно не мешает выполнению программы PSO и STABL. Однако иногда, когда оптимальное решение находится вблизи границы (как на рисунке 4), необходимо немного ослабить общую границу нового пространства (на 0.1 м) для правильной работы STABL. Пример показан на рис. 5. До релаксации (а) PSO ошибочно давал более высокое значение FS, чем в начальном испытании. После релаксации (b) PSO смог понизить FS по желанию.
Однако иногда, когда оптимальное решение находится вблизи границы (как на рисунке 4), необходимо немного ослабить общую границу нового пространства (на 0.1 м) для правильной работы STABL. Пример показан на рис. 5. До релаксации (а) PSO ошибочно давал более высокое значение FS, чем в начальном испытании. После релаксации (b) PSO смог понизить FS по желанию.
4. Результаты и обсуждение
В этом исследовании были проанализированы только 180 кинематически возможных направлений из 360 возможных направлений разреза склона (0°–359°). Два не смогли получить никаких значений FS с STABL (81° и 106°) и поэтому не были включены в последующий анализ.Рисунок 6 суммирует результаты. Это показывает, что минимальная FS, полученная в этом исследовании, составляет 0,985, а самый высокий процент улучшения с помощью PSO составляет 20,05%. За исключением нескольких выбросов, рисунок 6 показывает, что FS изменяется в зависимости от направления поперечного разреза, по-видимому, в соответствии с четко определенной тенденцией. Самые низкие значения FS наблюдались в диапазоне от 10° до 20°. Затем значение ПС быстро увеличивалось по мере удаления от этой области и примерно достигало максимума при 111° и 289°. Точки данных между 111° и 289° отсутствовали, поскольку движение склона в диапазоне этих направлений (в гору) было кинематически невозможно.Из рисунка 6 видно, что FS не является константой, а скорее зависит от направления свойства уклона. Поэтому использование «типичного» 2D-профиля для представления всего уклона в традиционном анализе устойчивости не совсем адекватно.
Самые низкие значения FS наблюдались в диапазоне от 10° до 20°. Затем значение ПС быстро увеличивалось по мере удаления от этой области и примерно достигало максимума при 111° и 289°. Точки данных между 111° и 289° отсутствовали, поскольку движение склона в диапазоне этих направлений (в гору) было кинематически невозможно.Из рисунка 6 видно, что FS не является константой, а скорее зависит от направления свойства уклона. Поэтому использование «типичного» 2D-профиля для представления всего уклона в традиционном анализе устойчивости не совсем адекватно.
4.1. Сравнение с предыдущими исследованиями на том же участке
Ниже представлены результаты анализа этого исследования и двух предыдущих исследований [4, 5]: (1) параллельные разрезы 0° [4]: минимальная FS среди 45 профилей составила 0,924.Процент улучшения по сравнению с исходным FS варьировался от 0,91% до 10,25%. (2) Параллельные резы под углом 45° [5]: минимальный FS среди 19 профилей составлял 1,130. Процент улучшения по сравнению с исходным FS варьировался от 0,16% до 11,11%. (3) Непараллельные срезы 0°–359°: минимальный FS среди 180 профилей составлял 0,985. Процент улучшения по сравнению с исходным FS варьировался от 0,05% до 20,05%. На рисунке 7 ниже сравниваются результаты анализа этих трех исследований. Используемый график «коробка с усами» показывает минимум, первый квартиль, медиану, третий квартиль и максимум наборов данных.Каждое исследование имеет два набора данных FS. Они представляют значения FS до и после применения алгоритма PSO к вычислению. Две самые левые группы на рисунке 7 представляют собой данные этого исследования, в то время как две средние группы относятся к профилям север-юг (азимут 0°) [4], а две крайние правые группы относятся к профилям поперечного сечения под углом 45° [5]. ]. Из рисунка 7 видно, что это исследование является наиболее полным из трех исследований. Он не только предоставляет наибольшее количество данных, но также охватывает самый широкий диапазон возможных значений FS.
Процент улучшения по сравнению с исходным FS варьировался от 0,16% до 11,11%. (3) Непараллельные срезы 0°–359°: минимальный FS среди 180 профилей составлял 0,985. Процент улучшения по сравнению с исходным FS варьировался от 0,05% до 20,05%. На рисунке 7 ниже сравниваются результаты анализа этих трех исследований. Используемый график «коробка с усами» показывает минимум, первый квартиль, медиану, третий квартиль и максимум наборов данных.Каждое исследование имеет два набора данных FS. Они представляют значения FS до и после применения алгоритма PSO к вычислению. Две самые левые группы на рисунке 7 представляют собой данные этого исследования, в то время как две средние группы относятся к профилям север-юг (азимут 0°) [4], а две крайние правые группы относятся к профилям поперечного сечения под углом 45° [5]. ]. Из рисунка 7 видно, что это исследование является наиболее полным из трех исследований. Он не только предоставляет наибольшее количество данных, но также охватывает самый широкий диапазон возможных значений FS. Вот ряд наблюдений: (1) Во всех трех исследованиях PSO улучшал (снижал) FS. Это успешная демонстрация применимости PSO при анализе устойчивости откосов. (2) 0,924 было самым низким значением FS, полученным в среднем исследовании, которое представляло параллельные разрезы север-юг в поперечном сечении. Самая низкая FS в исследовании от 0° до 359° была немного выше (но ненамного) и составила 0,985. Согласно (1), FS меньше единицы означает, что движущие силы, действующие на склон, больше, чем силы, противодействующие скользящему движению.Поскольку в обоих случаях значения FS (0,924 и 0,985) были меньше единицы, это указывает на нестабильность анализируемого уклона. (3) Две крайние правые группы на рис. 7 (представляющие исследование параллельных разрезов 45°) были наименее удовлетворительными. группа в сравнении. Минимальная FS, полученная в этом исследовании, была значительно выше, чем минимальная, полученная в двух других исследованиях. (4) На рисунке 7 также показано, что PSO постоянно улучшал FS, но процент улучшения в результате применения PSO был разным для всех трех исследований.
Вот ряд наблюдений: (1) Во всех трех исследованиях PSO улучшал (снижал) FS. Это успешная демонстрация применимости PSO при анализе устойчивости откосов. (2) 0,924 было самым низким значением FS, полученным в среднем исследовании, которое представляло параллельные разрезы север-юг в поперечном сечении. Самая низкая FS в исследовании от 0° до 359° была немного выше (но ненамного) и составила 0,985. Согласно (1), FS меньше единицы означает, что движущие силы, действующие на склон, больше, чем силы, противодействующие скользящему движению.Поскольку в обоих случаях значения FS (0,924 и 0,985) были меньше единицы, это указывает на нестабильность анализируемого уклона. (3) Две крайние правые группы на рис. 7 (представляющие исследование параллельных разрезов 45°) были наименее удовлетворительными. группа в сравнении. Минимальная FS, полученная в этом исследовании, была значительно выше, чем минимальная, полученная в двух других исследованиях. (4) На рисунке 7 также показано, что PSO постоянно улучшал FS, но процент улучшения в результате применения PSO был разным для всех трех исследований. исследований и варьируется от профиля к профилю.Это разумно, поскольку вычисление FS представляет собой очень сложную итеративную задачу (и нелинейную), выполняемую программой STABL. PSO использовался только для оптимизации граничных параметров, отправленных в программу STABL. (5) Из рисунка 7 трудно сделать вывод, какой тип анализа лучше всего подходит для других склонов в будущем. Анализ от 0° до 359° был наиболее полным, но анализ 0° привел к более низкому минимуму FS. Все они имели свои преимущества и недостатки. Кроме того, склоны будут иметь различный профиль поверхности земли и параметры грунта.Поэтому рисунок 7 не может дать каких-либо универсальных правил и применим к другим склонам в целом. Мы рекомендуем анализировать все склоны всеми возможными способами, используя автоматические процедуры, показанные в этом исследовании (и двух предыдущих исследованиях), чтобы получить убедительные результаты. составляет 0,924. Это результат анализа 244 (180 + 45 + 19) профилей поперечного сечения, и он должен иметь большое значение для этого уклона.
исследований и варьируется от профиля к профилю.Это разумно, поскольку вычисление FS представляет собой очень сложную итеративную задачу (и нелинейную), выполняемую программой STABL. PSO использовался только для оптимизации граничных параметров, отправленных в программу STABL. (5) Из рисунка 7 трудно сделать вывод, какой тип анализа лучше всего подходит для других склонов в будущем. Анализ от 0° до 359° был наиболее полным, но анализ 0° привел к более низкому минимуму FS. Все они имели свои преимущества и недостатки. Кроме того, склоны будут иметь различный профиль поверхности земли и параметры грунта.Поэтому рисунок 7 не может дать каких-либо универсальных правил и применим к другим склонам в целом. Мы рекомендуем анализировать все склоны всеми возможными способами, используя автоматические процедуры, показанные в этом исследовании (и двух предыдущих исследованиях), чтобы получить убедительные результаты. составляет 0,924. Это результат анализа 244 (180 + 45 + 19) профилей поперечного сечения, и он должен иметь большое значение для этого уклона. Это значение FS также должно дать пользователю гораздо более высокий уровень уверенности, чем полученный при анализе только одного «типичного» 2D-профиля уклона.
Это значение FS также должно дать пользователю гораздо более высокий уровень уверенности, чем полученный при анализе только одного «типичного» 2D-профиля уклона.
4.2. Произошло хорошее совпадение с оползнем
Анализ, представленный в этом исследовании, был основан на лазерном сканировании целевого склона в июне 2011 года. Анализ показал, что склон был неустойчивым. В августе 2012 г. после тайфуна Саола склон действительно сполз к северу [11, 12] в том же общем направлении, которое предсказывает рис. 6.Сползание склона обеспечивает убедительные физические доказательства в поддержку приведенного выше анализа.
4.3. Расширение до более сложных эволюционных алгоритмов
Техника, представленная в этом исследовании, представляет собой идеальное сочетание анализа устойчивости откосов (STABL) и эволюционных вычислений (PSO). Как упоминалось выше в методах исследования, решение для FS было сложной задачей, требующей итеративного подхода. Однако обращение с программой STABL как с вычислительной машиной и черным ящиком полностью избегало этой проблемы. Использование STABL вместо написания кодов для расчета FS также сделало результаты анализа более достоверными для целей сравнения. Использование комбинации PSO и STABL также означало, что не нужно было предпринимать дополнительные шаги, чтобы проверить, работают ли собственные коды так же хорошо и дают те же результаты, что и стандартная программа STABL. PSO не нужно было знать, как STABL решил FS. Он лишь «сказал» STABL, что нужно делать, чтобы добиться наилучших результатов. Другие, более сложные методы искусственного интеллекта, такие как искусственные нейронные сети (ИНС), неприменимы, поскольку они требуют большего взаимодействия с подпрограммами внутри программы STABL, что невозможно, поскольку STABL является коммерческим программным обеспечением, а не открытым исходным кодом.Поскольку ни один другой исследователь не пытался такого рода разделение двух тесно связанных компонентов в анализе устойчивости откосов, расчете FS (STABL) и оптимизации (PSO), прямое сравнение результатов этого исследования и других алгоритмов невозможно.
Использование STABL вместо написания кодов для расчета FS также сделало результаты анализа более достоверными для целей сравнения. Использование комбинации PSO и STABL также означало, что не нужно было предпринимать дополнительные шаги, чтобы проверить, работают ли собственные коды так же хорошо и дают те же результаты, что и стандартная программа STABL. PSO не нужно было знать, как STABL решил FS. Он лишь «сказал» STABL, что нужно делать, чтобы добиться наилучших результатов. Другие, более сложные методы искусственного интеллекта, такие как искусственные нейронные сети (ИНС), неприменимы, поскольку они требуют большего взаимодействия с подпрограммами внутри программы STABL, что невозможно, поскольку STABL является коммерческим программным обеспечением, а не открытым исходным кодом.Поскольку ни один другой исследователь не пытался такого рода разделение двух тесно связанных компонентов в анализе устойчивости откосов, расчете FS (STABL) и оптимизации (PSO), прямое сравнение результатов этого исследования и других алгоритмов невозможно. Однако могут существовать другие методы оптимизации прямого поиска, которые могут соответствовать результатам и производительности PSO в этом исследовании. Расширение текущего подхода PSO + STABL к другим эволюционным методам требует нового исследования.
Однако могут существовать другие методы оптимизации прямого поиска, которые могут соответствовать результатам и производительности PSO в этом исследовании. Расширение текущего подхода PSO + STABL к другим эволюционным методам требует нового исследования.
4.4. Полный поиск
Полный поиск проверяет каждую возможную точку в пространстве поиска. Авторы провели исчерпывающий поиск проблемы фиктивного уклона почвы (обычно используемый многими исследователями уклон для теоретических исследований и сравнения) в предыдущем исследовании [6]. Было проанализировано 5000 узлов сетки одного 2D-профиля в [6]. Аналогичный перебор проводился в данном исследовании для профиля (среди 180 профилей) с минимальной ПС (0,985), ориентированного на север под углом 18°.На рис. 8 показан трехмерный график поверхности вычисленных значений FS, тогда как на рис. 9 показано увеличенное изображение обведенной кружком части рис. 8. Вычисление заняло около четырех часов на компьютере Intel Core i7 (включая построение графика), и точка сетки была точной. до одного десятичного знака. Из результатов PSO, упомянутых ранее, было определено, что минимальная FS произошла в точке (15,900, 34,870) в мнимом пространстве (рис. 4). Сравнивая этот результат с результатами, показанными на рисунках 8 и 9, становится очевидным, что исчерпывающий поиск лишь приблизительно определил область, где может возникнуть минимальная FS (лицевая сторона рисунка 9).Он не определял точное местоположение, как метод PSO. Чтобы получить такое же точное решение, как PSO (от одного знака после запятой до трех знаков после запятой), потребовалось бы на = 10 000 вычислений больше, чем текущий полный перебор. Авторы не считают эти дополнительные вычисления полезными для данного исследования, потому что причиной выбора PSO в первую очередь было устранение огромных временных затрат. Если бы в этом исследовании использовался исчерпывающий поиск с точностью до трех знаков после запятой, то для одного профиля потребовался бы анализ в общей сложности 16 м 1000 решеток/м 16 м 1000 решеток/м = 256 000 000 решеток.
до одного десятичного знака. Из результатов PSO, упомянутых ранее, было определено, что минимальная FS произошла в точке (15,900, 34,870) в мнимом пространстве (рис. 4). Сравнивая этот результат с результатами, показанными на рисунках 8 и 9, становится очевидным, что исчерпывающий поиск лишь приблизительно определил область, где может возникнуть минимальная FS (лицевая сторона рисунка 9).Он не определял точное местоположение, как метод PSO. Чтобы получить такое же точное решение, как PSO (от одного знака после запятой до трех знаков после запятой), потребовалось бы на = 10 000 вычислений больше, чем текущий полный перебор. Авторы не считают эти дополнительные вычисления полезными для данного исследования, потому что причиной выбора PSO в первую очередь было устранение огромных временных затрат. Если бы в этом исследовании использовался исчерпывающий поиск с точностью до трех знаков после запятой, то для одного профиля потребовался бы анализ в общей сложности 16 м 1000 решеток/м 16 м 1000 решеток/м = 256 000 000 решеток. Поскольку было 180 профилей, потребовалось бы примерно 256 000 000 180 профилей = 46 080 000 000 узлов сетки. Программе STABL необходимо вызывать каждую точку сетки, при этом каждый вызов создает 100 круглых поверхностей для вычисления FS. Такие большие вычисления было трудно оправдать, и они противоречили эффективности использования PSO. Более того, результаты исследования [6], полученные с помощью PSO, не уступали лучшим результатам, полученным методом полного перебора. Этот важный вывод свидетельствует о том, что добавление исчерпывающего поиска не было ни необходимым, ни полезным для данного исследования.Это также не помогло бы понять ключевые моменты, изученные в этом исследовании, целью которого было изучить использование PSO для выполнения эффективного и действенного трехмерного анализа устойчивости откосов.
Поскольку было 180 профилей, потребовалось бы примерно 256 000 000 180 профилей = 46 080 000 000 узлов сетки. Программе STABL необходимо вызывать каждую точку сетки, при этом каждый вызов создает 100 круглых поверхностей для вычисления FS. Такие большие вычисления было трудно оправдать, и они противоречили эффективности использования PSO. Более того, результаты исследования [6], полученные с помощью PSO, не уступали лучшим результатам, полученным методом полного перебора. Этот важный вывод свидетельствует о том, что добавление исчерпывающего поиска не было ни необходимым, ни полезным для данного исследования.Это также не помогло бы понять ключевые моменты, изученные в этом исследовании, целью которого было изучить использование PSO для выполнения эффективного и действенного трехмерного анализа устойчивости откосов.
4.5. Случайность и сходимость
Типичная формулировка PSO имеет ряд параметров, таких как , , и которые можно настроить для повышения производительности или предотвращения локальных минимумов. Однако предыдущий пример исследования склона почвы [6] показал, что PSO быстро сходится (обычно только после десятков итераций), когда его применяли к анализу устойчивости склона.Более того, выбор параметров (таких как вес инерции) и случайные начальные значения почти не влияли ни на обнаружение глобального минимума, ни на производительность системы, пока выбранный вес инерции не был близок к нулю. В целях проверки был повторен тест на сходимость различных весов инерции (для = 0,0, 0,2, 0,4, 0,6, 0,8 и 1,0) для профиля с минимальной FS 0,985 в этом исследовании (как показано на рисунке 10). Результат очень похож на результат, полученный на фиктивном примере почвенного склона в [6].Как видно из рисунка 10, все кривые сходились быстро, и единственная кривая, не сошедшаяся к глобальному минимуму 0,985, принадлежит , как и ожидалось из [6]. Поскольку вес инерции оказывал лишь незначительное влияние на поведение сходимости (до тех пор, пока вес инерции не был равен нулю), авторы решили использовать число частиц, равное 30, при анализе остальных профилей.
Однако предыдущий пример исследования склона почвы [6] показал, что PSO быстро сходится (обычно только после десятков итераций), когда его применяли к анализу устойчивости склона.Более того, выбор параметров (таких как вес инерции) и случайные начальные значения почти не влияли ни на обнаружение глобального минимума, ни на производительность системы, пока выбранный вес инерции не был близок к нулю. В целях проверки был повторен тест на сходимость различных весов инерции (для = 0,0, 0,2, 0,4, 0,6, 0,8 и 1,0) для профиля с минимальной FS 0,985 в этом исследовании (как показано на рисунке 10). Результат очень похож на результат, полученный на фиктивном примере почвенного склона в [6].Как видно из рисунка 10, все кривые сходились быстро, и единственная кривая, не сошедшаяся к глобальному минимуму 0,985, принадлежит , как и ожидалось из [6]. Поскольку вес инерции оказывал лишь незначительное влияние на поведение сходимости (до тех пор, пока вес инерции не был равен нулю), авторы решили использовать число частиц, равное 30, при анализе остальных профилей.
Для тестирования различных начальных случайных начальных значений на рисунке 11 показаны результаты шести различных запусков (на рисунке показаны только шесть, чтобы избежать беспорядка).Опять же, все кривые быстро сходились к глобальному минимуму (менее 26 итераций). Это подтверждает вывод [6] о том, что влияние случайного начального числа также было незначительным. При внимательном рассмотрении рисунка 11 вместе с рисунками 8 и 9 причина такого результата ясна. Хотя вычисление FS с использованием модифицированного метода Бишопа (уравнения (3)) было итеративной и очень сложной процедурой, решение FS, показанное на рисунке 8, представляет собой относительно простую поверхность. Минимум этой поверхности располагался в тонкой области вблизи границы и вряд ли был пропущен, независимо от того, каким было начальное случайное затравочное число.
Общая производительность подхода, изложенного в этом документе, является удовлетворительной. Что еще более важно, PSO улучшал (снижал) FS в каждом случае. Более того, полученные результаты были максимально точными. Это связано с тем, что STABL выводит FS только до трех знаков после запятой. Поэтому дальнейшая настройка параметров PSO не даст более точного результата. Например, предположим, что минимальное значение FS равно 0,985 и соответствует точке (15,900, 34,870) в воображаемом пространстве.Если существовала точка, близкая к (15.900, 34.870) с еще более низким FS, она не будет обнаружена, потому что STABL вернет ту же FS 0,985 для новой точки. Поскольку FS одинаковы, входные параметры не будут корректироваться, и PSO не будет пытаться проводить дальнейшую оптимизацию. Это недостаток использования STABL в качестве блочного блока в вычислениях.
Более того, полученные результаты были максимально точными. Это связано с тем, что STABL выводит FS только до трех знаков после запятой. Поэтому дальнейшая настройка параметров PSO не даст более точного результата. Например, предположим, что минимальное значение FS равно 0,985 и соответствует точке (15,900, 34,870) в воображаемом пространстве.Если существовала точка, близкая к (15.900, 34.870) с еще более низким FS, она не будет обнаружена, потому что STABL вернет ту же FS 0,985 для новой точки. Поскольку FS одинаковы, входные параметры не будут корректироваться, и PSO не будет пытаться проводить дальнейшую оптимизацию. Это недостаток использования STABL в качестве блочного блока в вычислениях.
4.6. Другие родственные работы
PSO — это мощный, но простой метод оптимизации, который применялся во многих различных областях для решения множества различных типов задач, включая анализ устойчивости земляных откосов.Для земных склонов PSO в основном использовался для расчета минимальной FS и определения наиболее критической поверхности скольжения [13–20]. Помимо разработки теоретической основы, также был доступен ряд практических инженерных исследований. Например, Khajehzadeh et al. [16] произвели обратный расчет FS оползня в Улу-Кланге, Малайзия; Ван и др. [21] использовали PSO для оценки устойчивости плечевых отложений долины на левом берегу гидроэлектростанции Xiluodu в Китае; и Ли и др.[22] применили PSO к конструкции усиления высокого склона Чжунцзяу Трех ущелий. Однако большинство этих исследований, связанных с PSO, были основаны на 2D-профилях, и ни в одном из них не использовалось лазерное сканирование и STABL в анализе. Из этих исследований только одно рассматривало трехмерный анализ устойчивости откосов с помощью общей формы вращающегося эллипсоида [17]. Тем не менее, этот метод полностью отличался от подхода, использованного в этом исследовании, в котором анализировался наклон цели в направлениях от 0° до 359°.Первоначально в этом исследовании только предварительно анализировался наклон с использованием STABL в [11]. Позже анализ в [12] включал PSO с профилями, созданными вручную (вместо автоматически создаваемых профилей).
Помимо разработки теоретической основы, также был доступен ряд практических инженерных исследований. Например, Khajehzadeh et al. [16] произвели обратный расчет FS оползня в Улу-Кланге, Малайзия; Ван и др. [21] использовали PSO для оценки устойчивости плечевых отложений долины на левом берегу гидроэлектростанции Xiluodu в Китае; и Ли и др.[22] применили PSO к конструкции усиления высокого склона Чжунцзяу Трех ущелий. Однако большинство этих исследований, связанных с PSO, были основаны на 2D-профилях, и ни в одном из них не использовалось лазерное сканирование и STABL в анализе. Из этих исследований только одно рассматривало трехмерный анализ устойчивости откосов с помощью общей формы вращающегося эллипсоида [17]. Тем не менее, этот метод полностью отличался от подхода, использованного в этом исследовании, в котором анализировался наклон цели в направлениях от 0° до 359°.Первоначально в этом исследовании только предварительно анализировался наклон с использованием STABL в [11]. Позже анализ в [12] включал PSO с профилями, созданными вручную (вместо автоматически создаваемых профилей).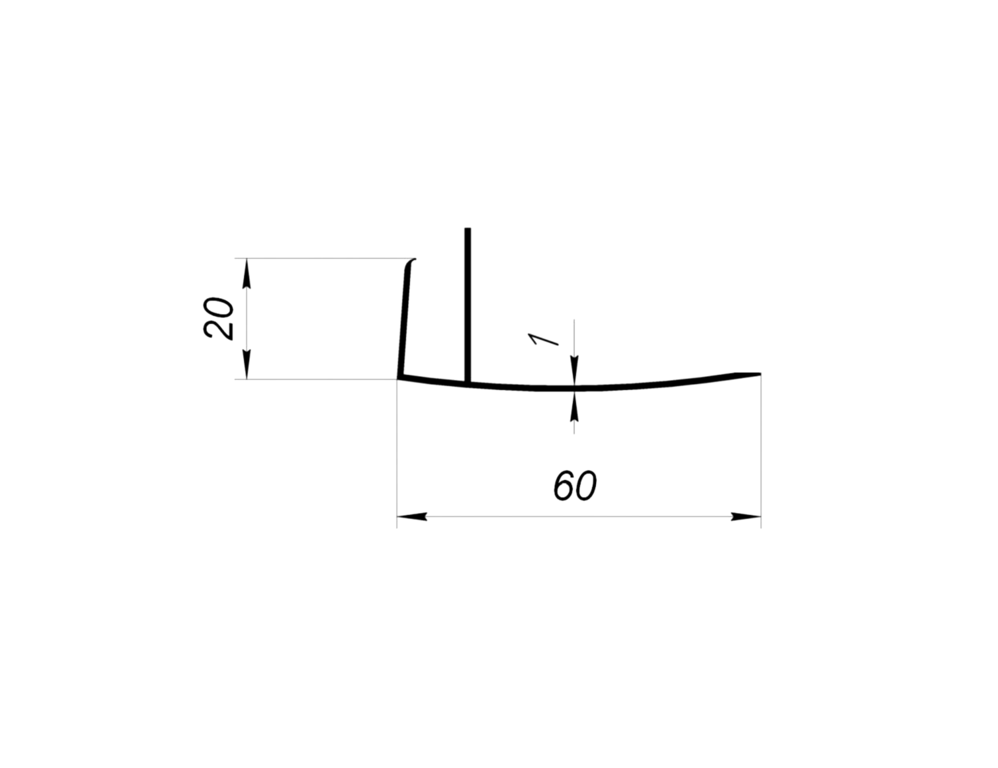 Общий комбинированный горизонтальный диапазон (левый и правый) склона в этих исследованиях составлял около 20 м, что было меньше, чем в текущем исследовании. Из-за различий в анализе значения FS в этих исследованиях отличались от значений FS в этом исследовании, в котором программа рассечения автоматически вырезала наклон и расширяла горизонтальные диапазоны.
Общий комбинированный горизонтальный диапазон (левый и правый) склона в этих исследованиях составлял около 20 м, что было меньше, чем в текущем исследовании. Из-за различий в анализе значения FS в этих исследованиях отличались от значений FS в этом исследовании, в котором программа рассечения автоматически вырезала наклон и расширяла горизонтальные диапазоны.
5. Резюме и выводы
Оползни представляют собой серьезную проблему, от которой страдают миллионы людей во всем мире. Цель этого исследования состояла в том, чтобы понять, как использование PSO может улучшить анализ сомнительных склонов до того, как произойдет оползень. Для создания трехмерных поверхностей грунта использовалось современное оборудование (наземный лазерный сканер), а для анализа устойчивости откосов использовалось стандартное прикладное программное обеспечение (STABL). Авторы также разработали собственные пользовательские программы для разрезания склона и создания профилей в различных направлениях.Основное использование алгоритма PSO заключалось в оптимизации параметров, связанных с границами склона, где начинаются и заканчиваются поверхности скольжения. Используя программу STABL в качестве вычислительного механизма, предлагаемая система могла считывать выходные файлы и автоматически генерировать новые входные файлы. С помощью этой возможности анализа стало возможным анализировать наклон в направлениях от 0° до 359°. Это исследование доказало, что полный анализ склона может быть выполнен автоматически. Таким образом, были сняты ограничения обработки склона как 2D-объекта и анализа только одного профиля поперечного сечения для представления всего склона.Результаты показали, что FS не является постоянным, а скорее зависит от направления свойства склона, и что более точная информация о состоянии склона получена в результате тщательного анализа уклона во многих направлениях. Вооружившись этой информацией, маловероятно, что в будущем инженеры будут игнорировать неустойчивые склоны. Это исследование также показало, что алгоритм PSO хорошо подходит для анализа устойчивости откосов. Суммируя это исследование и два предыдущих исследования того же участка, самая низкая FS анализируемого склона была равна 0.
Используя программу STABL в качестве вычислительного механизма, предлагаемая система могла считывать выходные файлы и автоматически генерировать новые входные файлы. С помощью этой возможности анализа стало возможным анализировать наклон в направлениях от 0° до 359°. Это исследование доказало, что полный анализ склона может быть выполнен автоматически. Таким образом, были сняты ограничения обработки склона как 2D-объекта и анализа только одного профиля поперечного сечения для представления всего склона.Результаты показали, что FS не является постоянным, а скорее зависит от направления свойства склона, и что более точная информация о состоянии склона получена в результате тщательного анализа уклона во многих направлениях. Вооружившись этой информацией, маловероятно, что в будущем инженеры будут игнорировать неустойчивые склоны. Это исследование также показало, что алгоритм PSO хорошо подходит для анализа устойчивости откосов. Суммируя это исследование и два предыдущих исследования того же участка, самая низкая FS анализируемого склона была равна 0. 924. Это результат анализа 244 (180 + 45 + 19) профилей поперечного сечения. Следовательно, это значение должно иметь большое значение и должно давать инженеру гораздо более высокий уровень уверенности.
924. Это результат анализа 244 (180 + 45 + 19) профилей поперечного сечения. Следовательно, это значение должно иметь большое значение и должно давать инженеру гораздо более высокий уровень уверенности.
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Благодарности
Это исследование было частично поддержано номерами грантов NSC 102-2221-E-027-077 и MOST 103-2221-E-027-052 от Национального научного совета и Министерства науки и технологий Тайваня.Финансовая поддержка высоко ценится.
Вода | Бесплатный полнотекстовый | Оценка влияния продольного профиля ручья на закон сопротивления потоку
2.1. Экспериментальные участки и измерения
Для проведения экспериментов использовали участок шириной 2 м и длиной 7 м (рис. 1), расположенный на экспериментальной территории Департамента сельского хозяйства, продовольствия и лесных наук Университета Палермо. Участок был подготовлен с тремя различными профилями (вогнутый, выпуклый и однородный) (рис. 1) с использованием среднего уклона участка s p , равного 18%.В частности, для вогнутого и выпуклого профилей участок был разделен на две части длиной 3,27 м, и были установлены два значения уклона (12 и 24 %), чтобы получить среднее значение 18 % (рис. 2). Почва представляла собой суглинок, характеризующийся содержанием глины, ила и песка 32,7%, 30,9% и 36,4% соответственно. Для всех профилей почву вручную рыхлили и сгребли, а затем уплотнили деревянным брусом. Насыпную плотность почвы определяли путем отбора проб почвы с помощью металлического цилиндра известного объема и определения ее массы после высыхания.Равномерный режим влажности почвы для всех опытов достигался увлажнением почвы до прекращения инфильтрации. Затем вручную нарезали борозды вдоль направления максимального уклона участка и формировали их с помощью расхода чистого потока 0,1 л с -1 , поданного в течение 3 мин. Ручьи имели такой же продольный профиль, как и участок. Для каждого ручья определяли девять продольных отрезков, ограниченных двумя поперечными сечениями, отстоящими друг от друга на 0,624 м (рис.
1) с использованием среднего уклона участка s p , равного 18%.В частности, для вогнутого и выпуклого профилей участок был разделен на две части длиной 3,27 м, и были установлены два значения уклона (12 и 24 %), чтобы получить среднее значение 18 % (рис. 2). Почва представляла собой суглинок, характеризующийся содержанием глины, ила и песка 32,7%, 30,9% и 36,4% соответственно. Для всех профилей почву вручную рыхлили и сгребли, а затем уплотнили деревянным брусом. Насыпную плотность почвы определяли путем отбора проб почвы с помощью металлического цилиндра известного объема и определения ее массы после высыхания.Равномерный режим влажности почвы для всех опытов достигался увлажнением почвы до прекращения инфильтрации. Затем вручную нарезали борозды вдоль направления максимального уклона участка и формировали их с помощью расхода чистого потока 0,1 л с -1 , поданного в течение 3 мин. Ручьи имели такой же продольный профиль, как и участок. Для каждого ручья определяли девять продольных отрезков, ограниченных двумя поперечными сечениями, отстоящими друг от друга на 0,624 м (рис. 3).
3).Постоянный чистый приток-сброс, начиная с 0.18 до 0,63 л с -1 , использовали для экспериментов.
Измерения глубины воды h, площади поперечного сечения σ, смоченного периметра C, уклона дна s и скорости течения V проводились для участков ручья (т. е. русла между данным измеренным поперечным сечением и концом ручья) на равномерные (99 п.), вогнутые (71 п.) и выпуклые (72 п.) борозды. Косвенные измерения числа Рейнольдса Re = V h/ν k , где ν k — кинематическая вязкость, числа Фруда F = V/√(gh), где g — ускорение свободного падения, и Дарси – Коэффициент трения Вейсбаха f = 8 gRs /V 2 , где R — гидравлический радиус.
Для каждой экспериментальной серии строили 3D-ЦМР участка участка по набору из 70 фотографий методом реконструкции 3D-фото в программе обработки изображений Agisoft Photoscan Professional (Версия 1.1.6, Агисофт, Санкт-Петербург) , Россия). Градиент уклона каждого сегмента ручья определялся с использованием тальвега ручья, полученного с помощью 3D-DTM. Уклон каждого участка ручья рассчитывался путем усреднения значений, измеренных на рассматриваемом участке.
Уклон каждого участка ручья рассчитывался путем усреднения значений, измеренных на рассматриваемом участке.
h=∑i=2N−1(σ12+σi+σN2)∑i=2N−1(w12+wi+wN2)
(1)
R=∑i=2N−1(σ12+σi+σN2)∑i=2N−1(C12+Ci+CN2)
(2)
где w — ширина поверхности, а N — количество поперечных сечений в зоне досягаемости.Раствор метиленового синего применяли в качестве индикатора красителя для измерения скорости потока [28, 37, 38, 39, 40]. Измеренная поверхностная скорость была преобразована в среднюю скорость потока V с поправочным коэффициентом 0,8 [41,42,43].
Измеренная поверхностная скорость была преобразована в среднюю скорость потока V с поправочным коэффициентом 0,8 [41,42,43].Для четырех ручьев каждой формы профиля цифровые модели рельефа (ЦМР) в конце этапа формирования (D1) и экспериментальных прогонов (D2) были получены из 3D-DTM. ЦМР разности (DoD) между D2 и D1 использовался для измерения значений глубины размыва внутри всего русла ручья и расчета общего объема размытого ручья RV.Учитывая, что минимальный уровень обнаружения используемых ЦМР составлял ±0,005 м, изменения высоты дна в диапазоне ±0,005 м не были обнаружены.
Наконец, для тех же ручьев были измерены значения глубины размыва SD с интервалом 0,005 м вдоль тальвега ручья, как разница высот между продольными профилями в конце этапа формообразования (D1) и в конце экспериментальные прогоны (D2) (пример для одной бороздки с выпуклой формой профиля показан на рис. 4). Для каждой борозды средняя глубина размыва SD м также была рассчитана как среднее значение SD.
2.2. Уравнение сопротивления ручьевому потоку
. Для течения в открытом русле профиль локальной скорости потока v(y) вдоль заданной вертикали представлен следующим функциональным соотношением [44,45,46]:φ(dvdy,y,h,d,u*,s,ρ,µ,g)=0
(3)
где φ — функциональный символ, v — местная скорость, y — расстояние от дна, d — характерный диаметр частиц пласта, u * = √(g R s) — скорость сдвига, ρ — плотность воды μ — динамическая вязкость воды.Применяя Π-теорему размерного анализа и используя в качестве размерных независимых переменных y, u * и µ, уравнение (3) можно выразить следующим безразмерным функциональным соотношением [30]:yu*dvdy=φ1(hd,s,u*yνk,Re,F)
(4)
в котором φ 1 — функциональный символ. Предполагая неполную автомодельность в u * y/ν k [25,47,48,49,50], пренебрегая влиянием Re (турбулентный режим течения) и учитывая, что число Фруда потока учитывает также отношение h/d [26], интегрирование уравнения (4) приводит к следующему профилю скорости:vu*=Γ(s,F) (u* yυk)δ
(5)
где Γ(s, F) — функция, определяемая измерениями скорости, а показатель степени δ рассчитывается по следующему теоретическому уравнению [51,52] Следующее выражение коэффициента трения Дарси-Вейсбаха f выводится [25,48,53] путем интегрирования уравнения (5):f=8 [21−δ Γ Reδ(δ+1) (δ+2)]−2/(1+δ)
(7)
Из профиля скорости (уравнение (5)) следующая оценка Γ v функции Γ [25, 53] получается путем установления равным α h расстояния y, на котором локальная скорость равна средней скорости в поперечном сечении V: Коэффициент α, который меньше 1, учитывает, что как V расположен ниже поверхности воды, так и учитывается профиль средней скорости в поперечном сечении. Коэффициент α должен быть рассчитан по следующему теоретическому соотношению, выведенному Ферро [25]:
Коэффициент α должен быть рассчитан по следующему теоретическому соотношению, выведенному Ферро [25]:α=[21−δ (δ+1) (δ+2)]1/δ
(9)
Для данного исследования α варьировалось в узком диапазоне и было принято среднее значение 0,124. Учитывая, что согласно уравнению (5) Γ теоретически зависит только от s и F [26, 54], Γ v можно оценить с помощью следующего уравнения мощности: где a, b и c — коэффициенты, определяемые из экспериментальных измерений.Схема размеров откосов и векторов сил для расчета уклона…
Контекст 1
… по устойчивости откосов для определения ранга приоритета фактора. Известные методы различаются формой расчетных поверхностей скольжения, способами определения сил, технологией расчета; однако принцип всех методов одинаков. Представляется, что результаты расчетов разными методами должны быть очень близкими. Наоборот, они сильно различаются. Рассчитаны по 8 методикам (Чугаева, Терзаги, Маслова, Бишопа, Фельни, М-П, Спенсера и Джамбу), коэффициенты устойчивости 6 глиняных откосов высотой 7-31 м, крутизной 19°-44°, 1. 7– 1,92 кН/м 3 , удельный вес 16–125 кПа, угол внутреннего трения 11–23° варьировали в пределах 1,00–4,35. Для сухих склонов максимальный коэффициент превышал минимальный до 3 раз, для насыщенных глин – до 2 раз (табл. 2). Метод Чугаева однозначно дает максимальные коэффициенты устойчивости, а метод Маслова — минимальные. Разница между максимальным и минимальным коэффициентами, рассчитанными по 6 методикам, достигает 24% от среднего значения коэффициента.Даже такое несоответствие неприемлемо при рассмотрении методов, считающихся достаточно надежными, и при применении их к практическим расчетам. Для выяснения причин этих различий все эти методы были проанализированы с акцентом на упрощения и их возможное влияние на результаты вычислений. Метод Чугаева основан на следующем упрощении: сила, прижимающая движущуюся массу откоса к скользкой поверхности F г (рис. искусственно. F 4), gn подставляется определенно Учитывается возрастающая сила тяжести как сила, наиболее устойчивая из надежных В широко используемом методе Терцаги такое грубое допущение не используется.
7– 1,92 кН/м 3 , удельный вес 16–125 кПа, угол внутреннего трения 11–23° варьировали в пределах 1,00–4,35. Для сухих склонов максимальный коэффициент превышал минимальный до 3 раз, для насыщенных глин – до 2 раз (табл. 2). Метод Чугаева однозначно дает максимальные коэффициенты устойчивости, а метод Маслова — минимальные. Разница между максимальным и минимальным коэффициентами, рассчитанными по 6 методикам, достигает 24% от среднего значения коэффициента.Даже такое несоответствие неприемлемо при рассмотрении методов, считающихся достаточно надежными, и при применении их к практическим расчетам. Для выяснения причин этих различий все эти методы были проанализированы с акцентом на упрощения и их возможное влияние на результаты вычислений. Метод Чугаева основан на следующем упрощении: сила, прижимающая движущуюся массу откоса к скользкой поверхности F г (рис. искусственно. F 4), gn подставляется определенно Учитывается возрастающая сила тяжести как сила, наиболее устойчивая из надежных В широко используемом методе Терцаги такое грубое допущение не используется.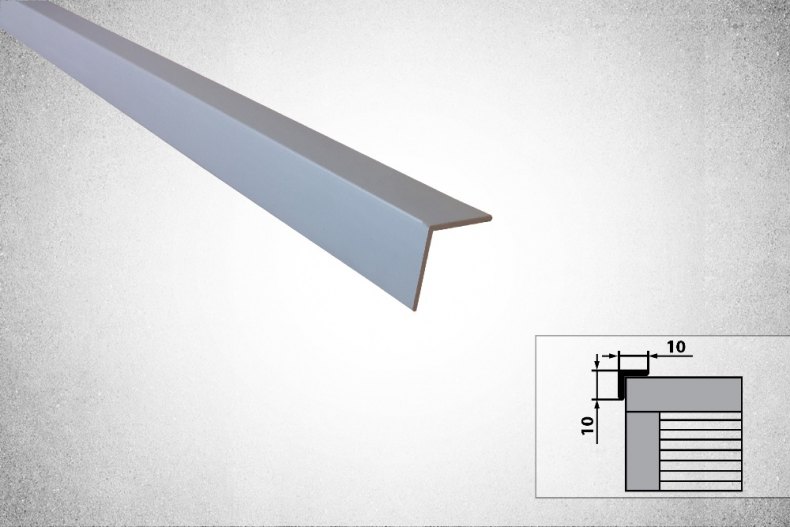 Каждый метод имеет свои несоответствия либо в форме профиля поверхности скольжения, либо в пренебрежении боковым касательным напряжением или другими допущениями, что вносит определенные ошибки, которые в конечном итоге приводят к отклонению результатов расчетов от реальной ситуации и снижению их достоверности. Во всех перечисленных выше методах давление грунтовых вод оценивается через одну силу на всю скользящую массу, т. е. силу, приложенную к центру тяжести массы. Сила порового давления обычно не принимается во внимание, когда процесс консолидации считается завершенным.Это и другие упрощения могут привести к значительным ошибкам в зависимости от степени важности неучтенного фактора для явления оползания склона. Устойчивость склона зависит от многих факторов, таких как высота H и угол наклона α, сцепление с, угол внутреннего трения φ грунта и расположение свободной поверхности грунтовых вод. Для определения влияния перечисленных факторов были проведены расчеты коэффициента устойчивости для ряда глинистых склонов с использованием программы GEOSLOPE.
Каждый метод имеет свои несоответствия либо в форме профиля поверхности скольжения, либо в пренебрежении боковым касательным напряжением или другими допущениями, что вносит определенные ошибки, которые в конечном итоге приводят к отклонению результатов расчетов от реальной ситуации и снижению их достоверности. Во всех перечисленных выше методах давление грунтовых вод оценивается через одну силу на всю скользящую массу, т. е. силу, приложенную к центру тяжести массы. Сила порового давления обычно не принимается во внимание, когда процесс консолидации считается завершенным.Это и другие упрощения могут привести к значительным ошибкам в зависимости от степени важности неучтенного фактора для явления оползания склона. Устойчивость склона зависит от многих факторов, таких как высота H и угол наклона α, сцепление с, угол внутреннего трения φ грунта и расположение свободной поверхности грунтовых вод. Для определения влияния перечисленных факторов были проведены расчеты коэффициента устойчивости для ряда глинистых склонов с использованием программы GEOSLOPE. За номинальные были приняты следующие параметры: уклон высотой 20 м и углом наклона 40°, сцеплением 20 кПа, углом внутреннего трения 20° и углом наклона плоскости впадины 20° (рис.4). Склон с такими параметрами типичен для литовских условий. Зависимость от параметров H , α , c , номинальных ter, φ и, скажем, β величин H составила , сохраняя исследуемую константу, оставшееся время и вычисляя изменение α , c , один φ , стабильность параметров и коэффициент β k для каждой величины переменный параметр. Расчеты проводились с 5-ю величинами переменной: минимальной, номинальной и максимальной и двумя графиками промежуточных (рис. 5) величин. Качественный и количественный рисунок признаков k – H/H от 0 зависимости были исследованы позже.Численные результаты вышеописанного исследования приведены в табл. 3. Соотношение максимальных и минимальных коэффициентов устойчивости откосов пока не позволяет делать обоснованных выводов, когда границы диапазонов параметров выбирались свободно, а приоритет факторов очевидна.
За номинальные были приняты следующие параметры: уклон высотой 20 м и углом наклона 40°, сцеплением 20 кПа, углом внутреннего трения 20° и углом наклона плоскости впадины 20° (рис.4). Склон с такими параметрами типичен для литовских условий. Зависимость от параметров H , α , c , номинальных ter, φ и, скажем, β величин H составила , сохраняя исследуемую константу, оставшееся время и вычисляя изменение α , c , один φ , стабильность параметров и коэффициент β k для каждой величины переменный параметр. Расчеты проводились с 5-ю величинами переменной: минимальной, номинальной и максимальной и двумя графиками промежуточных (рис. 5) величин. Качественный и количественный рисунок признаков k – H/H от 0 зависимости были исследованы позже.Численные результаты вышеописанного исследования приведены в табл. 3. Соотношение максимальных и минимальных коэффициентов устойчивости откосов пока не позволяет делать обоснованных выводов, когда границы диапазонов параметров выбирались свободно, а приоритет факторов очевидна. В анализируемых зависимостях превалируют факторы угла внутреннего трения грунта и угла наклона откоса. Следует пояснить, что сцепление исключительно сопротивляется скольжению только при большой величине φ = 0, поэтому в этом случае k max / k и min искажают получаемое исследуемое явление.Установлено, что однородные, k − H , k − α , все k − кривые c , k − были φ , а гладкие k − β и , графики плоские, что свидетельствует об отсутствии критических условий, при которых проскальзывание может произойти непредсказуемо. . Чтобы представить влияние процентных величин сил напора грунтовых вод в соотношениях (1), (2) и (3), они были рассчитаны для некоторой типичной литовской величины TT ρ α sf = = =781 =1622 1850 35° ; кНм; c кг/м = кНм; условия 20 наклон T 3 кПа; р и =0. стабильность T c φ Ноль =1079 = использование 31°; коэффициент влияния давления ГЕОСКЛОН: β кНм; = 30°; из этих плотность T τ воды =1545 ч. H из в = грунт 20 на кНм; поры…
В анализируемых зависимостях превалируют факторы угла внутреннего трения грунта и угла наклона откоса. Следует пояснить, что сцепление исключительно сопротивляется скольжению только при большой величине φ = 0, поэтому в этом случае k max / k и min искажают получаемое исследуемое явление.Установлено, что однородные, k − H , k − α , все k − кривые c , k − были φ , а гладкие k − β и , графики плоские, что свидетельствует об отсутствии критических условий, при которых проскальзывание может произойти непредсказуемо. . Чтобы представить влияние процентных величин сил напора грунтовых вод в соотношениях (1), (2) и (3), они были рассчитаны для некоторой типичной литовской величины TT ρ α sf = = =781 =1622 1850 35° ; кНм; c кг/м = кНм; условия 20 наклон T 3 кПа; р и =0. стабильность T c φ Ноль =1079 = использование 31°; коэффициент влияния давления ГЕОСКЛОН: β кНм; = 30°; из этих плотность T τ воды =1545 ч. H из в = грунт 20 на кНм; поры…
Новый метод выделения подножия континентального склона на основе комплексного анализа профилей
Алгоритм Дугласа-Пейкера и его усовершенствование
Алгоритм Дугласа-Пекера (сокращенно Д-П алгоритм), предложенный Дугласом и Томасом ( 1973) представляет собой алгоритм упрощения кривой, позволяющий значительно уменьшить количество избыточных точек, но сохраняющий основные характеристики кривой. Как правило, в этом алгоритме применяются рекурсивные функции. Однако это оказалось ненужным в процессе реализации программы, когда разработанная структура данных может хранить всю информацию до и после точек запроса на кривой.Еще один момент, который следует отметить, заключается в том, что значение начального отклонения расстояния (D) будет влиять на результат упрощения кривой. То есть большее значение приведет к удалению слишком большого количества деталей, тогда как меньшее значение приведет к плохому эффекту упрощения. Программа может автоматически регулировать значение D для быстрого, но хорошего упрощения кривой. Интегральный алгоритм является заметным преимуществом алгоритма Д-П, который может сохранять точки максимального изменения кривой; я.т. е. форма упрощенной кривой остается неизменной, что удовлетворяет требованию идентификации ФОС. Для идентификации точки FOS необходимо найти точку измерения глубины воды с максимальным изменением градиента, которая также является точкой экстремума второй производной на топографическом профиле, расположенной в точке поворота от материкового склона к океанической котловине.
Как правило, в этом алгоритме применяются рекурсивные функции. Однако это оказалось ненужным в процессе реализации программы, когда разработанная структура данных может хранить всю информацию до и после точек запроса на кривой.Еще один момент, который следует отметить, заключается в том, что значение начального отклонения расстояния (D) будет влиять на результат упрощения кривой. То есть большее значение приведет к удалению слишком большого количества деталей, тогда как меньшее значение приведет к плохому эффекту упрощения. Программа может автоматически регулировать значение D для быстрого, но хорошего упрощения кривой. Интегральный алгоритм является заметным преимуществом алгоритма Д-П, который может сохранять точки максимального изменения кривой; я.т. е. форма упрощенной кривой остается неизменной, что удовлетворяет требованию идентификации ФОС. Для идентификации точки FOS необходимо найти точку измерения глубины воды с максимальным изменением градиента, которая также является точкой экстремума второй производной на топографическом профиле, расположенной в точке поворота от материкового склона к океанической котловине.
Технический метод
Метод определения FOS должен быть точным, количественным и поддающимся проверке. Настоящий метод строит серию топографических профилей вертикально к направлению простирания континентального склона, а затем определяет точки FOS в соответствии с изменениями подводного топографического профиля.Однако трудно сделать определение только на основе топографического профиля, MCS или SDG; следовательно, для комплексного анализа местоположения точек FOS необходимы другие источники информации. Поэтому предлагаемый метод называется TSDPIA.
FOS, определяемая как топографическая точка с максимальным изменением градиента (UN 1993, 1999), соответствует точке экстремума второй производной, а не точке нулевого значения профиля градиента; таким образом, ФОС часто не является точкой экстремума топографического профиля.Более того, результат сравнения показывает, что точка экстремума второй производной всегда находится вблизи точки экстремума топографического профиля, но в норме они не перекрываются.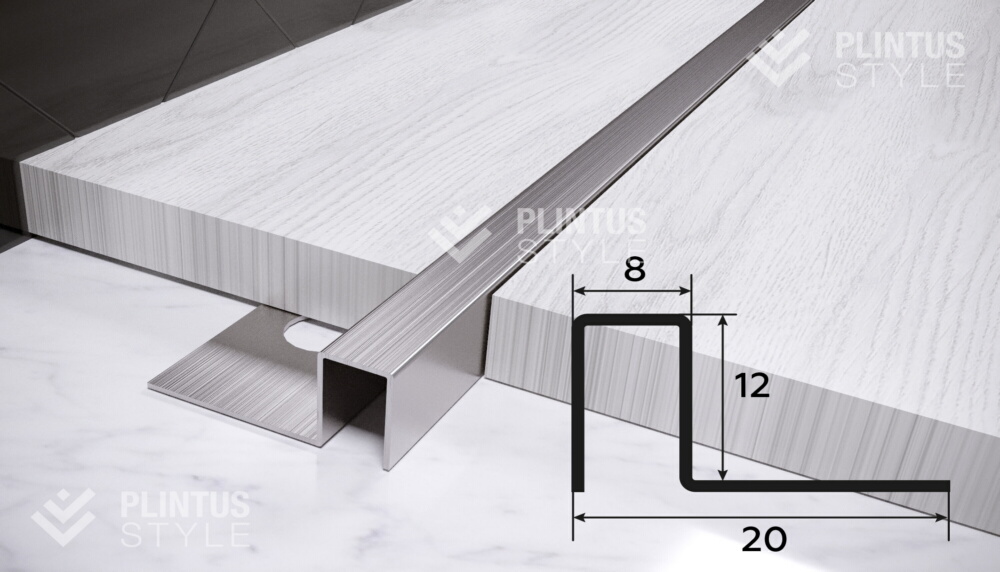 Топографический профиль, на котором расположена точка FOS, имеет выпуклую форму (продольная ось направлена в сторону увеличения глубины воды). Следовательно, точка с экстремальным и положительным значением второй производной является потенциальной точкой FOS. Из-за влияния мелкомасштабной топографии топографический профиль может иметь несколько точек экстремума второй производной, и поэтому исходный топографический профиль необходимо упростить.
Топографический профиль, на котором расположена точка FOS, имеет выпуклую форму (продольная ось направлена в сторону увеличения глубины воды). Следовательно, точка с экстремальным и положительным значением второй производной является потенциальной точкой FOS. Из-за влияния мелкомасштабной топографии топографический профиль может иметь несколько точек экстремума второй производной, и поэтому исходный топографический профиль необходимо упростить.
Типичный топографический профиль континентальной окраины состоит из трех участков (рис. 2): плоского и мелководного континентального шельфа, крутого континентального склона с резким изменением глубины и плоского и глубоководного -глубина океанического бассейна. ЛОС находится в точке поворота от материкового склона к океанической котловине, где глубина воды относительно велика, а градиент соответственно больше к материковому склону и меньше к океанической котловине.Для исходного топографического профиля, находящегося под влиянием мелкомасштабной локальной топографии, может быть несколько точек, соответствующих упомянутым выше условиям.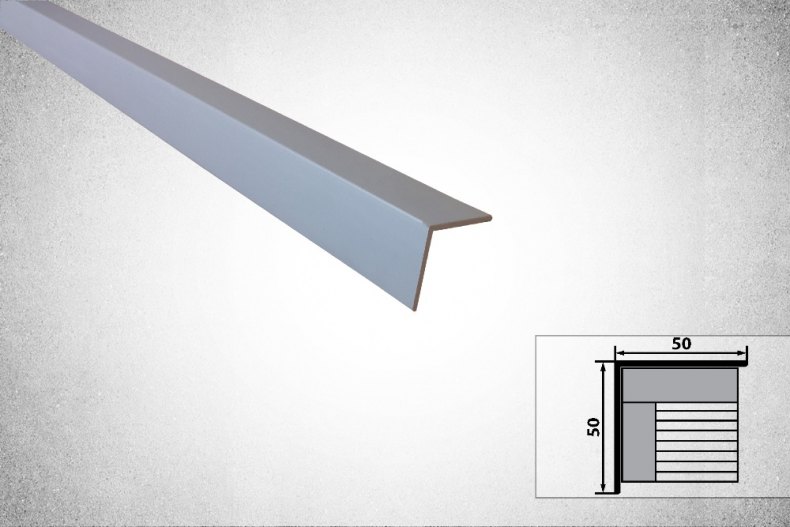 Поэтому исходный профиль следует упростить, чтобы исключить влияние местной топографии.
Поэтому исходный профиль следует упростить, чтобы исключить влияние местной топографии.
Комплексный профиль для определения FOS
Фильтрация может сгладить исходный топографический профиль и упростить определение FOS. Однако у него есть потенциальный недостаток, заключающийся в том, что основные характеристики исходного топографического профиля могут быть изменены.Напротив, с помощью точек экстремума и квадратичной аппроксимации алгоритма D-P можно не только упростить исходный топографический профиль, но и сохранить его черты. Алгоритм D-P имеет значительное преимущество, заключающееся в сохранении самых основных характеристик кривой, в то время как трудно напрямую определить местоположение FOS, просто подобрав исходный топографический профиль. Точка, выбранная алгоритмом Д-П, может не быть точкой экстремума второй производной кривой, т.е.т. е. алгоритм Д-П может удалить точку экстремума второй производной во время фильтрации. Следовательно, перед подгонкой алгоритма Д-П мы должны подобрать исходный профиль на основе точки экстремума второй производной, а затем применить алгоритм Д-П для выполнения квадратичной подгонки на основе профиля точки экстремума. Таким образом, можно гарантировать, что каждая полученная точка является точкой экстремума второй производной, что позволяет избежать ложной точки FOS.
Следовательно, перед подгонкой алгоритма Д-П мы должны подобрать исходный профиль на основе точки экстремума второй производной, а затем применить алгоритм Д-П для выполнения квадратичной подгонки на основе профиля точки экстремума. Таким образом, можно гарантировать, что каждая полученная точка является точкой экстремума второй производной, что позволяет избежать ложной точки FOS.
Путем вычисления второй производной топографического профиля D–P можно получить новый профиль градиента и профиль второй производной.Профиль после двух процессов упрощения сохраняет только самые основные характеристики кривой без вмешательства мелкомасштабной местной топографии. Следовательно, мы можем анализировать особенности каждой точки на профиле D–P, включая глубину воды, градиент, вторую производную, вогнуто-выпуклую характеристику и корреляцию (непрерывность) между точкой и ее соседними точками на верхний склон, нижний склон и глубину воды, а затем судить, соответствует ли топографическое изменение типичным характеристикам (сегментации) точки поворота от континентального склона к океаническому бассейну.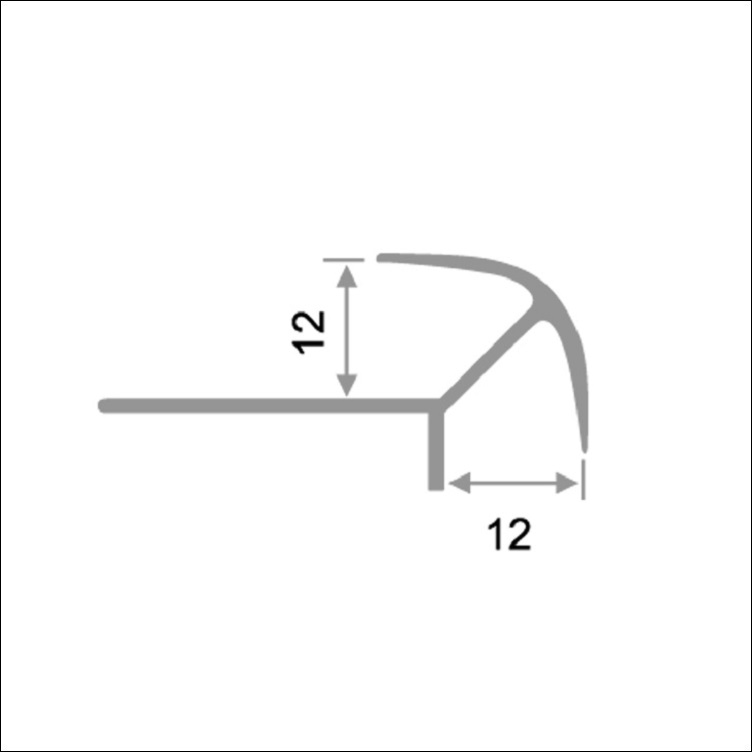 С помощью этих параметров мы можем точно определить расположение точек FOS на кривой (рис. 2).
С помощью этих параметров мы можем точно определить расположение точек FOS на кривой (рис. 2).
Технический процесс
Для заданной цифровой модели глубины сетки (DDM) точка FOS может быть идентифицирована автоматически, выполнив семь шагов (включая разрезание сетки, первую деривацию, начальное топографическое упрощение, второе топографическое упрощение, вторую деривацию, устранение вогнутости местности, комплексное суждение) и шесть критериев (рис. 3), которые обсуждаются ниже.
Рис. 3Техпроцесс идентификации ФОС
Этап 1: Резка по сетке
Исходный топографический профиль g 0 получается с помощью серии прямых линий для разрезания цифровой модели глубины и последующего расчета пересечения. Полученный топографический профиль должен соответствовать признаку «континентальный шельф – материковый склон – океанический бассейн» (рис. 3, 4(а)).
Рис. 4
4 Типовой топографический профиль и процесс идентификации ВОС ( а исходный топографический профиль; б профиль точки экстремума; в профиль Д-П; d вогнуто-исключенный профиль и идентифицированный ФОС)
Этап 2: Первая производная
Профиль уклона и второй производный профиль получаются путем вычисления производной кривой топографического профиля.Тогда расстояние, топография, градиент и вторая производная профиля вместе образуют набор данных G 0 (рис. 3, 4(а)).
Шаг 3: Начальное топографическое упрощение
Сохраняются только точки экстремума второго производного профиля, координаты которых вместе с точками данных глубины воды образуют новый упрощенный топографический профиль g 1 и новый набор данных Г 1 . По сравнению с исходным топографическим профилем можно обнаружить, что может быть сохранена только точка данных глубины воды, которая соответствует характеристике точки экстремума второй производной (рис. 3, 4(б)).
3, 4(б)).
Шаг 4: Второе топографическое упрощение
Применяя алгоритм Д-П для обработки первоначально упрощенного топографического профиля g 1 , мы можем получить новый набор данных G 2 , который удовлетворяет нашим требованиям и формирует новый топографический профиль г 2 . Второй упрощенный топографический профиль g 2 сохраняет лишь небольшую часть точек данных, соответствующих требованиям (рис. 3, 4(в)).
Шаг 5: Вторая производная
Путем вычисления производной топографического профиля g 2 (второй производной) формируются новый градиентный профиль и второй производный профиль (рис.3).
Шаг 6: Исключение вогнутого рельефа
Используя второй цикл для проверки всех точек данных в топографическом профиле g 2 , можно исключить точки с вогнутыми элементами для формирования нового набора данных G 3 . Из этого формируются новый топографический профиль g 3 , новый градиентный профиль и профиль второй производной (рис. 3, 4(d)).
3, 4(d)).
Этап 7: Комплексная оценка
С помощью шагов (1)–(6) получается упрощенный интегрированный профиль.После двух процессов упрощения и устранения вогнутости топографический профиль значительно упрощается, при этом континентальный шельф и океанический бассейн представляют собой плоский рельеф, а континентальный склон показывает особый градиент. Затем мы можем изучить топографический профиль g 3 , чтобы определить точки FOS в соответствии со следующими шестью критериями (рис. 3).
Критерии a: Градиент
Классифицируя значения градиента различных точек профиля, мы можем получить средние градиенты континентального шельфа, океанического бассейна и континентального склона соответственно; затем мы можем определить область континентального склона на основе разницы градиентов.
Критерий b: Глубина воды
Классифицируя глубину воды в различных точках профиля, мы можем получить среднее значение глубины воды континентального шельфа и океанического бассейна; таким образом, идентифицируя континентальный шельф и океанический бассейн.
Критерий c: Вторая производная
Точка FOS – это точка с максимальным изменением уклона от континентального склона к океаническому бассейну, которая также является точкой экстремума второй производной.
Критерий d: Выпуклость
Расположенная в точке поворота от континентального склона к океаническому бассейну, FOS представляет собой выпуклость, т.е.т. е. точка FOS также является точкой данных с положительным значением второй производной.
Критерий е: Сегментация
Учитывая, что соседние точки до и после точки ЛОС относятся соответственно к материковому склону и океанической котловине, можно предварительно судить о расположении ЛОС по сегментированным перепадам уклона материкового склона и океанический бассейн.
Критерий f: Непрерывность
В соответствии с правилом, согласно которому точки с одинаковым градиентом расположены близко друг к другу, каждая точка профиля будет расти по направлению к начальной и конечной точкам профиля и записывать расстояние своего роста от их. Следовательно, точка с максимальным расстоянием роста является точкой FOS.
Следовательно, точка с максимальным расстоянием роста является точкой FOS.
В конце концов, точки данных, полученные с помощью вышеуказанных семи шагов и отвечающие шести критериям, идентифицируются как точки FOS.
Оценка влияния литологических условий, характеристик блоков и топографии склонов на длину распространения камнепадов в Альпах и на острове Реюньон
Abellán, A., Vilaplana, JM, Calvet, J., García-Sellés, Д. и Асенсио Э.: Мониторинг камнепадов с помощью наземного лазерного сканирования – тематическое исследование поверхности базальтовой скалы в Кастельфоллит-де-ла-Рока (Каталония, Испания), Nat.Опасности Земля Сист. Sci., 11, 829–841, https://doi.org/10.5194/nhess-11-829-2011, 2011.
Альярди, Ф. и Кроста, ГБ: Трехмерное численное моделирование камнепадов с высоким разрешением, Междунар. Дж. Рок Мех. Min., 40, 455–471, https://doi.org/10.1016/S1365-1609(03)00021-2, 2003.
Azzoni, A. and de Freitas, MH: экспериментально полученные параметры, решающие для породы анализ падения, Rock Mech. Rock Eng., 28, 111–124, https://doi.org/10.1007/BF01020064, 1995.
Rock Eng., 28, 111–124, https://doi.org/10.1007/BF01020064, 1995.
Bennett, G.Л., Молнар П., Эйзенбайс Х. и МакАрделл Б.В.: Сила эрозии в швейцарских Альпах: характеристика обрушения склонов в Ильграбене, Earth Surf. проц. Land., 37, 1627–1640, https://doi.org/10.1002/esp.3263, 2012.
Caine, N.: Текстура осыпи в Тасмании, J. Sediment. Res., 37, 796–803, https://doi.org/10.1306/74D717A3-2B21-11D7-8648000102C1865D, 1967.
Caviezel, A., Demmel, SE, Ringenbach, A., Bühler, Y., Лу Г., Кристен М., Диннин К.Э., Эберхард Л.А., фон Рикенбах, Д., и Бартельт, П.: Реконструкция четырехмерных траекторий камнепада с использованием дистанционного зондирования и акселерометров и гироскопов, основанных на скалах, Earth Surf. Dynam., 7, 199–210, https://doi.org/10.5194/esurf-7-199-2019, 2019.
Conrad, O., Bechtel, B., Bock, M., Dietrich, H. , Fischer, E., Gerlitz, L., Wehberg, J., Wichmann, V., и Böhner, J.: Система для автоматизированного геолого-научного анализа (SAGA) v. 2.1.4, Geosci. Model Dev., 8, 1991–2007 гг., https://doi.org/10.5194/gmd-8-1991-2015, 2015 г.
2.1.4, Geosci. Model Dev., 8, 1991–2007 гг., https://doi.org/10.5194/gmd-8-1991-2015, 2015 г.
Копонс, Р., Вилаплана, Дж. М., и Линарес, Р.: Анализ расстояния прохождения камнепада с использованием эмпирических моделей (Сола д’Андорра-ла-Велья, Центральные Пиренеи), Nat. Опасности Земля Сист. Sci., 9, 2107–2118, https://doi.org/10.5194/nhess-9-2107-2009, 2009.
Cox, NJ: Оценка ядра как основной инструмент для анализа геоморфологических данных, Earth Surf. проц. Land., 32, 1902–1912, https://doi.org/10.1002/esp.1518, 2007.
Кроста, Г. Б., Альярди, Ф., Фраттини, П., и Лари, С.: Ключевые вопросы моделирования камнепадов, оценки опасности и риска для защиты от камнепадов, в: Инженерная геология для общества и территории, 2, Оползневые процессы, под ред.: Лоллино, Г., Джордан, Д., Кроста, Г., Короминас, J., Azzam, R., Wasowski, J., и Sciarra, N., Springer, International Publishing, Cham, Heidelberg, New York, Dordrecht, London, Switzerland, 43–58, https://doi.org/10. 1007 /978-3-319-09057-3_4, 2015.
1007 /978-3-319-09057-3_4, 2015.
Цуй, Ш., Пей, Xj., и Хуанг, Rq.: Характер качения камнепада на пологом склоне: экспериментальный подход, J.Mt.Sci., 14, 1550–1562, https://doi.org/10.1007/s11629-016-4144-7, 2017.
Dietze, M., Mohadjer, S., Turowski, JM, Ehlers, TA и Ховиус, Н.: Сейсмический мониторинг небольших альпийских камнепадов – достоверность, точность и ограничения, Earth Surf. Dynam., 5, 653–668, https://doi.org/10.5194/esurf-5-653-2017, 2017.
Dietze, M., Turowski, JM, Cook, KL, и Hovius, N.: Пространственно-временные закономерности, триггеры и анатомия сейсмически обнаруженных камнепадов, Earth Surf. Dynam., 5, 757–779, https://doi.org/10.5194/esurf-5-757-2017, 2017.
Доррен, Л.К.А.: Обзор механики камнепадов и подходов к моделированию, Prog. физ. Geog., 27, 69–87, https://doi.org/10.1191/0309133303pp359ra, 2003.
Durand, V., Mangeney, A., Haas, F., Jia, X., Peltier, A., Хиберт К., Ферраццини В., Ковальски П., Лоре Ф., Брюне К., Сатриано К. , Вегнер К., Делорм А., Бонилья Ф. и Вильнёв Н. : О связи между внешними воздействиями и нестабильностью склона в кратере на вершине Питон-де-ла-Фурнез, остров Реюньон, J Geophys Res: Earth Surface, 123, 2422–2442, https://doi.org/10.1029/2017JF004507, 2018.
, Вегнер К., Делорм А., Бонилья Ф. и Вильнёв Н. : О связи между внешними воздействиями и нестабильностью склона в кратере на вершине Питон-де-ла-Фурнез, остров Реюньон, J Geophys Res: Earth Surface, 123, 2422–2442, https://doi.org/10.1029/2017JF004507, 2018.
Фарин, М., Манжени, А., Туссен, Р., де Рони, Дж., Шапиро, Н., Девез, Т., Хиберт, К., Матон, К. , Седан О. и Бергер Ф.: Характеристика камнепадов по сейсмическому сигналу: результаты лабораторных экспериментов, J. Geophys. рез.-сол. Ea., 120, 7102–7137, https://doi.org/10.1002/2015JB012331, 2015.
Фэн Л., Пацци В., Интриери Э., Гракки Т. и Джильи Г. : Анализ сейсмических характеристик камнепадов на основе полевых испытаний: частота, амплитуда и продолжительность, Дж.Mt.Sci., 16, 955–970, https://doi.org/10.1007/s11629-018-5286-6, 2019.
Фитиус, С.Г., Джакомини, А., и Буцци, О.: Значение геологии по морфологии потенциально неустойчивых горных пород, инж. Geol., 162, 43–52, https://doi.org/10.1016/j.enggeo.2013. 05.007, 2013.
05.007, 2013.
Франку, Б. и Манте, К.: Анализ сегментации в профиле альпийских осыпные склоны, Permafrost Periglac., 1, 53–60, https://doi.org/10.1002/ppp.3430010107, 1990.
Frattini, P., Crosta, G.Б. и Альярди Ф.: Характеристика и моделирование камнепадов, в: Оползни, типы, механизмы и моделирование, ред.: Клаг, Дж. Дж. и Стед, Д., Издательство Кембриджского университета, Кембридж, Соединенное Королевство, 267–281, https ://doi.org/10.1017/CBO9780511740367.023, 2012.
Gerber, E.: Klassifikation von Schutthalden, Geogr. Helv., 29, 73–82, https://doi.org/10.5194/gh-29-73-1974, 1974.
Гловер, Дж., Бартельт, П., Кристен, М., и Гербер, В. .: Моделирование камнепада с неправильными каменными блоками, в: Инженерная геология для общества и территории, Том 2, под ред.: Лоллино, Г., Джордан, Д., Кроста, ГБ, Короминас, Дж., Аззам, Р., Васовски, Дж., и Скиарра, Н., Спрингер, International Publishing, Cham, Heidelberg, New York, Dordrecht, Лондон, Швейцария, 1729–1733 гг. , https://doi.org/10.1007/978-3-319-09057-3_306, 2015.
, https://doi.org/10.1007/978-3-319-09057-3_306, 2015.
Грачев И. и Саэйди С.: Влияние неровностей поверхности на падение движение горных пород, Геомеханика и геоинженерия, 14, 52–58, https://doi.org/10.1080/17486025.2018.1508857, 2019.
Герин, А., Сток, Г.М., Радью, М.Дж., Джабоедофф, М., Коллинз, Б.Д., Маташи, Б., Авдиевич, Н., и Деррон, М.-Х.: Количественная оценка 40-летней активности камнепадов в долине Йосемити с помощью исторической фотограмметрии «Структура из движения» и наземное лазерное сканирование, Geomorphology, 356, 1–18, https://doi.org/10.1016/j.geomorph.2020.107069, 2020.
Haas, F., Heckmann, T., Wichmann, V., and Becht , М.: Анализ биения крупного камнепада в Доломитовых Альпах/Итальянских Альпах с использованием размеров и форм частиц, полученных с помощью LIDAR, Earth Surf.проц. Land., 37, 1444–1455, https://doi.org/10.1002/esp.3295, 2012.
Heckmann, T., Bimböse, M., Krautblatter, M., Haas, F., Becht, M. ., и Морче, Д.: От геотехнического анализа к количественной оценке и моделированию с использованием данных LiDAR: исследование камнепадов в водосборе Рейнталя, Баварские Альпы, Германия, Earth Surf. проц. Land., 37, 119–133, https://doi.org/10.1002/esp.2250, 2012.
проц. Land., 37, 119–133, https://doi.org/10.1002/esp.2250, 2012.
Heiser, M., Scheidl, C., and Kaitna, R.: Концепции оценки для сравнения наблюдаемых и смоделированных области осаждения движений масс, Вычисл.Geosci., 21, 335–343, https://doi.org/10.1007/s10596-016-9609-9, 2017.
Hergarten, S., Robl, J., and Stüwe, K.: Извлечение топографической полосы профили по искривленным геоморфологическим элементам, Earth Surf. Dynam., 2, 97–104, https://doi.org/10.5194/esurf-2-97-2014, 2014.
Hibert, C., Mangeney, A., Grandjean, G., and Shapiro, NM : Нестабильность склона кратера Доломье, остров Реюньон: от сейсмических сигналов до характеристик камнепада, J. Geophys. Рез., 116, 1–18, https://doi.org/10.1029/2011JF002038, 2011.
Ибер, К., Манжени, А., Гранжан, Г., Пельтье, А., Димуро, А., Шапиро, Н.М., Ферраццини, В., Буасье, П., Дюран, В. ., и Ковальски, П.: Пространственно-временная эволюция активности камнепадов с 2007 по 2011 год на вулкане Питон-де-ла-Фурнез по сейсмическим данным, J. Volcanol. Геот. Res., 333-334, 36–52, https://doi.org/10.1016/j.jvolgeores.2017.01.007, 2017.
Volcanol. Геот. Res., 333-334, 36–52, https://doi.org/10.1016/j.jvolgeores.2017.01.007, 2017.
Хунгр, О. и Эванс, С.Г.: Инженерная оценка опасности осколочных камнепадов, в : Материалы 5-го Международного симпозиума по оползням, Лозанна, Швейцария, 10–15 июля 1988 г., 894318, 685–690, 1988.
Джабоедофф, М. и Деррон, М.-Х.: Оценка опасностей в рамках интегрированного процесса оценки риска оползней (IRAPL), в: Материалы Международной конференции по управлению рисками оползней, Ванкувер, Канада, 31 мая – 3 июня. 2005, 2005.
Джабоедофф М., Мецгер Р., Оппикофер Т., Кутюр Р., Деррон М.-Х., Локат Дж. и Турмел Д.: Новые методы анализа рельефа горных пород с использованием ЦМР и Трехмерное изображение точек помутнения: программное обеспечение COLTOP-3D, в: Труды 1-го канадско-американского симпозиума по механике горных пород, Ванкувер, Канада, 27–31 мая 2007 г., ARMA-07-008, 61–68, 2007 г.
Jaboyedoff, M. and Labiouse, V.: Техническое примечание: Предварительная оценка зон выхода камнепадов, Nat. Опасности Земля Сист. Sci., 11, 819–828, https://doi.org/10.5194/nhess-11-819-2011, 2011.
Опасности Земля Сист. Sci., 11, 819–828, https://doi.org/10.5194/nhess-11-819-2011, 2011.
Ji, Z.-M., Chen, Z.-J., Niu, Q .-H., Wang, T.-J., Song, H. и Wang, T.-H.: Лабораторное исследование влияющих факторов и их контроль коэффициента восстановления во время камнепадов, Landslides, 16, 1939 –1963, https://doi.org/10.1007/s10346-019-01183-x, 2019.
Джомелли, В.и Франку, Б.: Сравнение характеристик рельефа камнепадных осыпей и снежных лавин в альпийской среде с использованием нового методологического подхода: Massif des Ecrins, French Alps, Geomorphology, 35, 181–192, https://doi.org/10.1016 /S0169-555X(00)00035-0, 2000.
Kenner, R.: Процессы массового истощения, затрагивающие поверхность склона альпийской осыпи: годовой бюджет наносов за 2009–2018 гг. на перевале Флюела, восточные Швейцарские Альпы, Земля Деград. Дев., 31, 451–462, https://doi.org/10.1002/ldr.3462, 2019.
Киркби, М.Дж. и Стэтхэм, И.: Движение камней на поверхности и образование осыпей, J. Geol., 83, 349–362, https://www.jstor.org/stable/30059027 (последний доступ: 8 февраля 2021 г.) , 1975.
Geol., 83, 349–362, https://www.jstor.org/stable/30059027 (последний доступ: 8 февраля 2021 г.) , 1975.
Knoblich, K.: Über den Böschungswinkel von Schutthalden, Catena, 2, 1–10, https://doi.org/10.1016/S0341-8162(75)80001-4, 1975.
Kotarba, А. и Стрёмквист, Л.: Процессы транспортировки, сортировки и отложения альпийских отложений обломков склонов в польских Татрах, Geogr. Аня. А, 66, 285–294, https://doi.org/10.1080/04353676.1984.11880116, 1984.
Krautblatter M. and Dikau R.: К единой концепции для сравнения и экстраполяции отступления каменных стен и подачи камнепадов, Geogr. Аня. A, 89, 21–40, https://doi.org/10.1111/j.1468-0459.2007.00305.x, 2007.
Кромер, Р., Уолтон, Г., Грей, Б., Лата, М. ., and Group, R.: Разработка и оптимизация автоматизированной системы фиксированного фотограмметрического мониторинга склонов горных пород, Remote Sens., 11, 1–18, https://doi.org/10.3390/rs11161890, 2019.
Lambert, S., Bourrier, F., and Toe, D.: Улучшение кодов трехмерного моделирования траектории камнепада для оценки эффективности защитных насыпей, Int. Дж. Рок Мех. Min., 60, 26–36, https://doi.org/10.1016/j.ijrmms.2012.12.029, 2013.
Дж. Рок Мех. Min., 60, 26–36, https://doi.org/10.1016/j.ijrmms.2012.12.029, 2013.
Лейне Р.И., Швейцер А., Кристен М., Гловер Дж., Бартельт, П., и Гербер, В.: Моделирование траекторий камнепада с учетом формы скалы, Multibody Syst. Дин., 32, 241–271, https://doi.org/10.1007/s11044-013-9393-4, 2014.
Ленат Ж.-Ф., Башелери П. и Мерль О.: Анатомия вулкана Питон-де-ла-Фурнез (Реюньон, Индийский океан), Бык. Volcanol., 74, 1945–1961, https://doi.org/10.1007/s00445-012-0640-y, 2012.
Лукман, Б.Х.: Процессы, перенос, отложения и формы рельефа: камнепад, в: Горные и Геоморфология холмов, Трактат по геоморфологии, под редакцией: Шредера, Дж. Ф., Стоффеля, М., и Марстона, Р. А., Справочный модуль по системам Земли и наукам об окружающей среде, 7, 174–182, https://doi.org/10.1016/B978-0-12-374739-6.00162-7, 2013a.
Лукман, Б. Х.: Склоны осыпей, изд.: Элиас, С. А., Энциклопедия четвертичной науки, 3, 566–573, Elsevier, Амстердам, 2013b.
Meißl, G.: Modellierung der Reichweite von Felsstürzen, Fallbeispiele zur GIS-gestützten Gefahrenbeurteilung aus dem Bayerischen und Tiroler Alpenraum, докторская диссертация, Институт географии, Университет Инсбрука, Австрия, 249 стр. , 1998.
, 1998.
Merle 900 ., Мэрин П., Мишон Л., Башелери П.и Смитана, М.: Кальдеры, оползни и палеоканьоны на вулкане Питон-де-ла-Фурнез (остров Реюньон, Индийский океан), J. Volcanol. Геот. Res., 189, 131–142, https://doi.org/10.1016/j.jvolgeores.2009.11.001, 2010.
Мессенцель, К. и Дико, Р.: Структурный и тепловой контроль частоты и величины камнепадов в пределах каменно-осыпных систем (Швейцарские Альпы), Earth Surf. проц. Land., 42, 1963–1981, https://doi.org/10.1002/esp.4155, 2017.
Микош М., Петье У. и Рибичич М.: Применение программы моделирования камнепадов в альпийской долине в Словении, в материалах Международного симпозиума INTERPRAEVENT по смягчению последствий стихийных бедствий, связанных с селевыми потоками, обвалами склонов и оползнями, Ниигата, Япония, 25–27 сентября 2006 г., 199–211, 2006 г.
Наппи, М., Будетта, П., Ломбарди, Г. и Минотта, К.: Оценка выбега камнепадов, сравнение эмпирических и траекторных подходов, в: Наука и практика оползней, том 6: Оценка рисков, управление и смягчение последствий, ред. : Марготини, К., Канути П. и Сасса К., Springer, Berlin, Heidelberg, Germany, 177–182, https://doi.org/10.1007/978-3-642-31319-6_25, 2013.
: Марготини, К., Канути П. и Сасса К., Springer, Berlin, Heidelberg, Germany, 177–182, https://doi.org/10.1007/978-3-642-31319-6_25, 2013.
Okura, Ю., Китахара Х., Саммори Т. и Каванами А.: Влияние объема камнепада на расстояние выбега, англ. Geol., 58, 109–124, https://doi.org/10.1016/S0013-7952(00)00049-1, 2000.
Пельтье, А., Башелери, П., и Штаудахер, Т.: Магма транспортировка и хранение в Питон-де-ла-Фурнез (Реюньон) в период с 1972 по 2007 год: обзор геофизических и геохимических данных, J.вулкан. Геот. Рез., 184, 93–108, https://doi.org/10.1016/j.jvolgeores.2008.12.008, 2009a.
Пельтье, А., Штаудашер, Т., Башелери, П. и Кайоль, В.: Формирование обрушения кальдеры в апреле 2007 г. на вулкане Питон-де-ла-Фурнез: анализ данных GPS, J. Volcanol. Геот. Рез., 184, 152–163, https://doi.org/10.1016/j.jvolgeores.2008.09.009, 2009b.
Пельтье, А., Вильнёв, Н., Ферраццини, В., Тестуд, С., Хассен, Т., Буасье, П. и Катрин, П.: Изменения в долгосрочных геофизических предвестниках извержения в Питон-де- la Fournaise: Последствия для управления реагированием, Фронт. Earth Sci., 6, https://doi.org/10.3389/feart.2018.00104, 2018.
Earth Sci., 6, https://doi.org/10.3389/feart.2018.00104, 2018.
Перес, Ф.Л.: Ткань осыпи и морфология частиц на пике Лассен, Калифорния, Геогр. Аня. A, 71, 43–57, https://doi.org/10.2307/521007, 1989.
Перес, Флорида: Ткань осыпи, морфология обломков и ботанические индикаторы склоновых процессов на скалах Хаоса (Калифорнийские каскады), США , геогр. физ. Quatern., 52, 1–22, https://doi.org/10.7202/004861ar, 1998.
Пфайффер, Т.Дж. и Боуэн, Т.Д.: Компьютерное моделирование камнепадов, Бюллетень Ассоциации инженеров-геологов, 26, 135– 146, https://doi.org/10.2113/gseegeosci.xxvi.1.135, 1989.
Попеску Р., Веспремеану-Строй А., Онака А., Василе М., Крусеру Н. и Поп О.: Малая высота исследование вечной мерзлоты в системе переохлажденных осыпей склон-скальный ледник в Румынских Карпатах (Детуната-Гоала, горы Апусени), Геоморфология, 295, 840–854, https://doi.org/10.1016/j.geomorph.2017.07.029, 2017 .
Рапп, А.: Недавнее развитие горных склонов в Кяркевагге и окрестностях, северная Скандинавия, Геогр. Анн., 42, 65–200, https://doi.org/10.1080/20014422.1960.11880942, 1960.
Анн., 42, 65–200, https://doi.org/10.1080/20014422.1960.11880942, 1960.
Раванель, Л., Аллиньол, Ф., Делин, П., Грубер, С. и Равелло, М.: Камнепады в массиве Монблан в 2007 и 2008 гг., Оползни, 7, 493–501, https://doi.org/10.1007/s10346-010-0206-z, 2010.
RIEGL Laser Measurement Systems GmbH: Технические данные, RIEGL LMS-Z420i, Хорн, Австрия, 2010 г.
RIEGL Laser Measurement Systems GmbH: Data Sheet, RIEGL VZ-4000, Horn, Austria, 2020.
Royán, MJ, Abellán, A., Jaboyedoff, M., Вилаплана, Дж. М., и Кальвет, Дж.: Пространственно-временной анализ деформации перед камнепадом с использованием наземного лидара, оползни, 11, 697–709, https://doi.org/10.1007/s10346-013-0442-0 , 2014.
Руис-Карулла, Р. и Короминас, Дж.: Анализ камнепадов с помощью модели фрактальной фрагментации, Rock Mech. Rock Eng., 53, 1433–1455, https://doi.org/10.1007/s00603-019-01987-2, 2020.
Сала З., Хатчинсон Д.Дж. и Харрап Р.: Моделирование фрагментарного камнепады, обнаруженные с помощью наземного лазерного сканирования со склонов скал в южно-центральной части Британской Колумбии, Канада, Нац. Опасности Земля Сист. Sci., 19, 2385–2404, https://doi.org/10.5194/nhess-19-2385-2019, 2019.
Опасности Земля Сист. Sci., 19, 2385–2404, https://doi.org/10.5194/nhess-19-2385-2019, 2019.
Сандип, К.С., Луо, Л., и Сенетакис, К.: Влияние размера зерна и Шероховатость поверхности при нормальном коэффициенте восстановления одиночных зерен, Материалы, 13, 814, https://doi.org/10.3390/ma13040814, 2020.
Сандерс, Д., Остерманн, М., и Крамерс, Дж. : Четвертичные карбонатно-каменистые осыпные последовательности склонов (Восточные Альпы, Австрия): осадочные фации и фациальная архитектура, Facies, 55, 345–373, https://doi.org/10.1007/s10347-008-0175-z, 2009.
Сенс-Шенфельдер, К., Помпони, Э., и Пельтье, А.: Динамика вулкана Питон-де-ла-Фурнез, наблюдаемая с помощью интерферометрии пассивных изображений с несколькими эталонами, Дж. Вулканол. Геот. Res., 276, 32–45, https://doi.org/10.1016/j.jvolgeores.2014.02.012, 2014.
Серрано, Э. Санхосе, Дж. Дж., Гомес-Гутьеррес, А., и Гомес-Ленде , М.: Поверхностное движение и каскадные процессы на обломочных конусах в умеренных высокогорьях (Пикос-де-Европа, северная Испания), Sci. Total Environ., 649, 1323–1337, https://doi.org/10.1016/j.scitotenv.2018.08.405, 2019.
Total Environ., 649, 1323–1337, https://doi.org/10.1016/j.scitotenv.2018.08.405, 2019.
Statham, I.: Развитие склона осыпи в условиях движения поверхностных частиц, TI Brit. Geogr., 59, 41–53, https://doi.org/10.2307/621711, 1973.
Statham, I.: Модель камнепада на осыпном склоне, Earth Surf. Proc., 1, 43–62, https://doi.org/10.1002/esp.32
Staudacher, T., Peltier, A., Ferrazzini, V., Di Muro, A., Boissier, П., Кэтрин П., Ковальски П., Лорет Ф.и Лебретон, Дж.: Пятнадцать лет интенсивной изверженной активности (1998–2013 гг.) вулкана Питон-де-ла-Фурнез: обзор, в: Активные вулканы юго-западной части Индийского океана. Питон де ла Фурнез и Картала, ред.: Башелери, П., Ленат, Ж.-Ф., Ди Муро, А., и Мишон, Л., Springer, Берлин, Гейдельберг, Германия, 139–170, https:/ /doi.org/10.1007/978-3-642-31395-0_9, 2016.
Струнден, Дж., Элерс, Т.А., Брем, Д., и Неттесхайм, М.: Пространственные и временные вариации камнепадов, определенные с помощью TLS измерения в дегляциированной долине, Швейцария, J. Геофиз. Рез. Earth Surf., 120, 1251–1273, https://doi.org/10.1002/2014JF003274, 2015.
Геофиз. Рез. Earth Surf., 120, 1251–1273, https://doi.org/10.1002/2014JF003274, 2015.
Урай, М., Геши, Н., и Штаудахер, Т.: Оценка размера и объема обрушения кальдеры на вулкане Питон-де-ла-Фурнез во время извержения в апреле 2007 г. с использованием стереоизображений ASTER, Geophys. Рез. Lett., 34, 1944–8007, https://doi.org/10.1029/2007GL031551, 2007.
Valeton, I.: Beziehungen zwischen petrographischer Beschaffenheit, Gestalt und Rundungsgrad einiger Flussgerölle (Зависимости между немного гравия), Petermann Geogr.Mitt., 99, 13–17, 1955.
Vanneschi, C., Di Camillo, M., Aiello, E., Bonciani, F., and Salvini, R.: Фотограмметрия SfM-MVS для анализа камнепадов и оценки опасности по древнеримской дороге Via Flaminia в ущелье Фурло (Италия), ISPRS Int. Geo-Inf., 8, 1–23, https://doi.org/10.3390/ijgi8080325, 2019.
Вилахосана И., Суриньяч Э., Абеллан А., Хазарадзе Г., Гарсия Д. ., и Льоса, Дж.: Сейсмические сигналы, вызванные камнепадом: тематическое исследование в Монтсеррате, Каталония, Nat. Опасности Земля Сист.Sci., 8, 805–812, https://doi.org/10.5194/nhess-8-805-2008, 2008.
Опасности Земля Сист.Sci., 8, 805–812, https://doi.org/10.5194/nhess-8-805-2008, 2008.
Volkwein, A., Schellenberg, K., Labiouse, V., Agliardi, F. , Berger, F., Bourrier, F., Dorren, LKA, Gerber, W., and Jaboyedoff, M.: Характеристика камнепадов и структурная защита – обзор, Nat. Опасности Земля Сист. Sci., 11, 2617–2651, https://doi.org/10.5194/nhess-11-2617-2011, 2011.
Volkwein, A., Brügger, L., Gees, F., Gerber, W. , Крумменахер, Б., Куммер, П., Лардон, Дж., и Саттер, Т.: Повторное тестирование траектории камнепада, Науки о Земле, 8, 1–27, https://doi.org/10.3390/geosciences8030088, 2018.
Wang, I.-T. и Ли, К.-Ю.: Влияние формы склона и шероховатости поверхности на траектории движения одиночного камнепада, Всемирная академия наук, инженерии и технологий, Международный журнал гражданского, экологического, структурного, строительного и архитектурного проектирования, 4, 122–128, 2010.
Wang, Y., Jiang, W., Cheng, S., Song, P., and Mao, C.: Влияние угла удара на коэффициент восстановления при анализе камнепадов на основе среднемасштабный лабораторный тест, Nat. Опасности Земля Сист. Sci., 18, 3045–3061, https://doi.org/10.5194/nhess-18-3045-2018, 2018.
Опасности Земля Сист. Sci., 18, 3045–3061, https://doi.org/10.5194/nhess-18-3045-2018, 2018.
White, SE: Альпийские формы массового движения (некатастрофические): классификация, описание и значение, Arctic Alpine Res., 13, 127–137, https://doi.org/10.2307/1551190, 1981.
Whitehouse, IE and McSaveney, MJ: Диахронные осыпные поверхности в Южных Альпах, Новая Зеландия, и их влияние на осыпные отложения, Arctic Alpine Res., 15, 53–64, https://doi.org/10.2307/1550981, 1983.
Wichmann, V.: Модель Gravitational Process Path (GPP) (v1.0) – система моделирования гравитационных процессов на основе ГИС, Geosci. Model Dev., 10, 3309–3327, https://doi.org/10.5194/gmd-10-3309-2017, 2017.
Ямамото Т., Такада А., Исидзука Ю., Мияджи Н. ., и Tajima, Y.: Базальтовые пирокластические потоки вулкана Фудзи, Япония: характеристики отложений и их происхождение, Бюлл. Вулканол., 67, 622–633, https://doi.org/10.1007/s00445-004-0398-y, 2005.
Зевенберген, Л.В. и Торн, Ч.

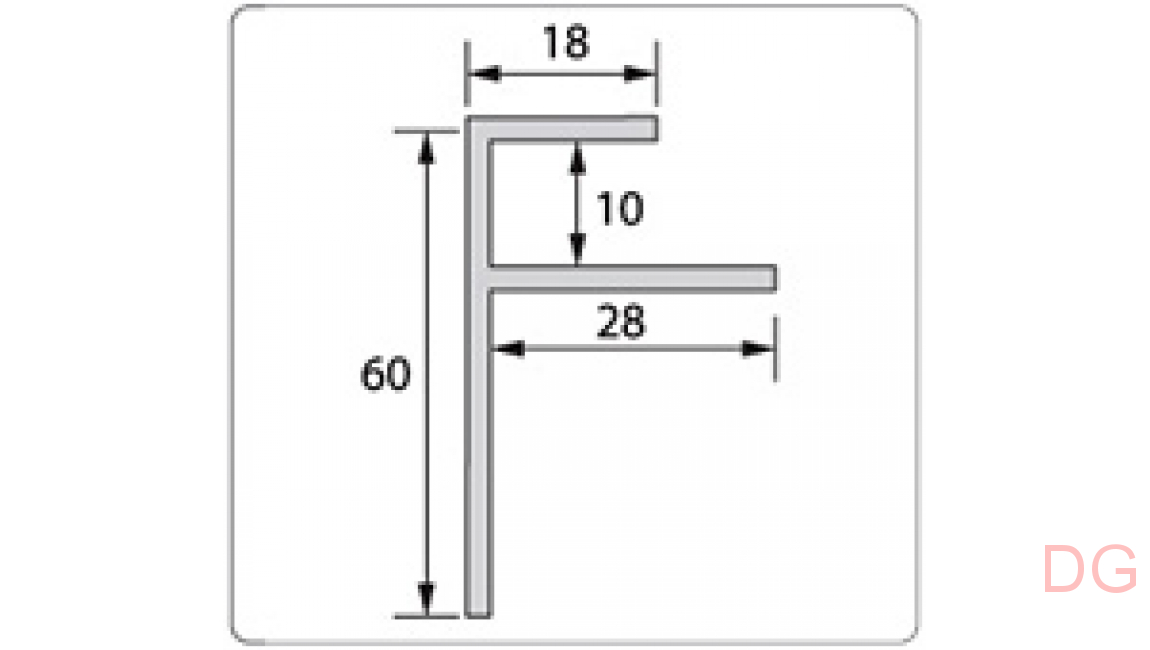 С этой целью можно использовать специальный строительный нож.
С этой целью можно использовать специальный строительный нож.
